UC Berkeley非监督学习--自回归模型

    想系统学习一下生成网络，开个新坑，翻译整理一下UC Berkeley非监督学习的课程。这篇翻译第二讲Autoregressive Models，自回归模型。

    这个课程总共十二讲，官方链接：

https://sites.google.com/view/berkeley-cs294-158-sp20/home

    目前已整理过：

        Lecture 1：UC Berkeley非监督学习–介绍

        Lecture 7：自监督学习（Self Supervised Learning）

    这篇会讲一些非常简单的生成网络，比如histogram，还有最新的一些基于神经网络的自回归模型。

    我们先考虑一个问题，一个长宽分别为128个像素的彩色图片，可以用多少维空间中的一个位置（点）来表达，答案是大概是五万维。模型的目标是可以得到复杂高维数据的分布。并实现计算上和统计上的高效性，计算上的高效性是计算可以快速完成，统计上的高效是指不需要太多数据，模型就可以得到正确的分布。

看具体的模型。

1. Histogram

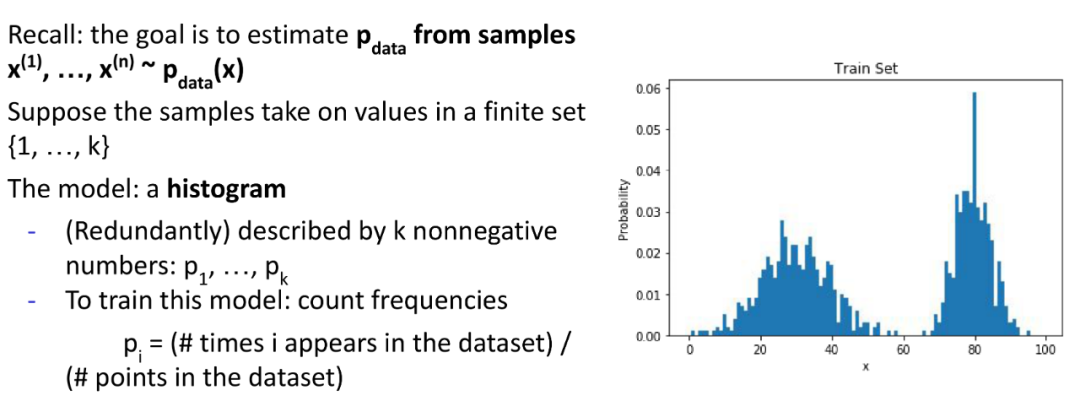
这里举个例子说这个算法可能会容易懂一点，假设你接了一个案子，预测华山山顶每天的最低气压，精确到个位数就行，然后你得到了最近三年每一天华山山顶上的最低气压，但只有一个气压值，对应的时间丢失了，然后你要用Histogram算法来预测明天华山山顶的最低气压值。有了这些数据，你可以得到每个气压值在过去三年中出现的次数，频率。也就得到了最低气压值的概率分布。在没有其他常识或者先验知识的情况下，你根据Histogram算法给出的答案，就是有最高概率的最低气压值。

接下来看Inference和Sampling要怎么完成：

Inference是推理出数据的概率，比如你有一个气压值，Inference就是推理这个气压作为最低气压值的概率。

Sampling是抽样，抽样的方法是，首先计算总概率，一般是1，然后在0-1之间按均匀分布随机取一个数u，Fi计算的是P1-Pi的总和，所以从P1开始加上P2，加上P3，当加到Pi时，发现Fi恰好大于或者等于产生的随机数u，那么这个i就是要抽出的样本。

一维空间的数据可以用这样的算法解决，那么多维空间的呢？

多维空间就不行，举个例子，比如我们有个数据集叫MNIST，里面都是二值图，即每个像素点的值都是0或1，那么可能的图有多少种呢？2的784次方个。所以如果你对这样一个数据集画直方图，横坐标有2的784次方个值，而这个数据集中的图片远没有这么多，因此就目前的现实情况，根本无法用Histogram的方式来计算概率分布。

那么对于一维空间的数据，Histogram是个不错的算法吗？很明显也不是的。通常都会像下图中左边的样子，train set和test set，Histogram的结果虽然看着形状相似，但是有些值差别会特别大。

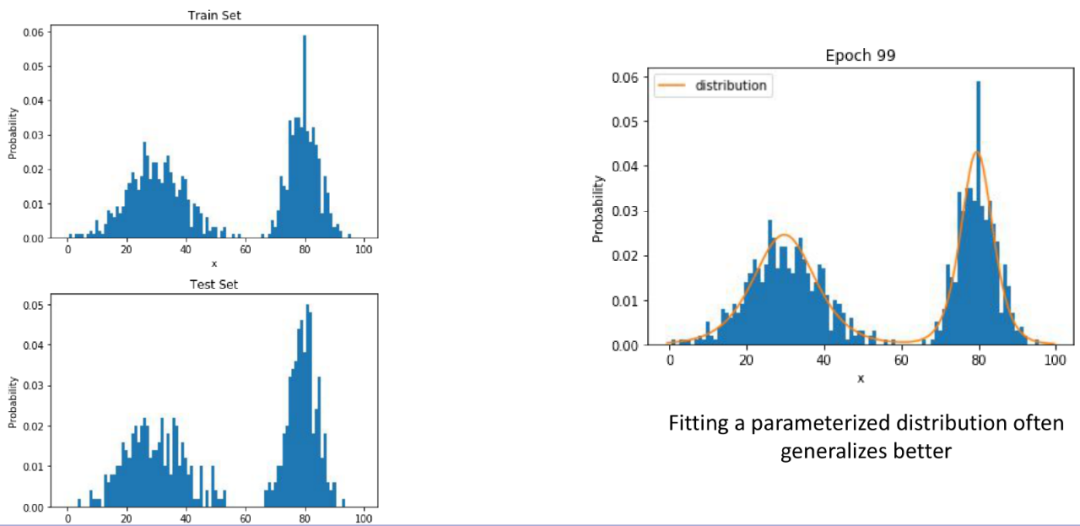
因此，如果可以产生一个更平滑的分布结果，综合考虑每个值周边的概率分布来确定自己的概率分布的话，也许能更好地匹配测试集的概率分布。

2. Parameterized Distributions and Maximum Likelihood 

因此，与其去求变量的概率分布，不如去求概率分布函数。

每个变量理论上都有一个概率分布函数，而通常这个函数是不容易被解出来的，我们可以做到的就是做很多很多假设，看看每个假设在现有数据集上的效果，然后用在现有数据集上表现最佳的那个假设来作为变量的概率分布函数。

要完成上面的任务，需要解决两个问题，一是怎么做假设，另外一个问题是怎么怎么用现有的数据集评估假设。

假设的话，可以根据一些经验设定，比如解决图像识别问题，可以用卷积神经网络。而假设的评估，则需要损失函数。

一般用来设计损失函数，有极大似然估计和KL散度（参考：Cross Entropy Loss）。这里用极大似然估计说明，我们的目的是求概率分布函数，比如一个图像识别问题，其中一个假设是一个三层的卷积网络可以做这个任务，但构成这个网络需要一堆参数，这些参数一开始是未知的，所以问题就变成了，如何求这些参数，使得这个函数可以更好地用作现有数据的概率分布函数。那这个待求参数的网络，假设（其实带不同参数的网络也可以被看成不同的假设），函数，我们也可以称为似然函数。那如何评估不同参数下的函数，方法其实很简单，就是最大化现有样本的出现的概率（既然这个样本曾经出现过，那么我们认为，它有很高的概率再次出现，如果这个样本曾经多次出现，那么它应该会有更高的概率会再次出现）。

完成极大似然估计或者KL散度，可以用SGD算法。

除了极大似然估计，在设计损失函数的时候，用贝叶斯加入先验函数也是常使用的方法。

3. Autoregressive Model

极大似然估计是频率派，也就是说是完全基于现有数据来评估模型，而贝叶斯属于贝叶斯派，会加入一些先验知识。

举个例子，比如事件A是世界即将毁灭，假设P(A) = 0.000001，事件B是太阳从西边升起，假设P(B) = 0.0000001，假设如果世界即将毁灭，太阳会从西边升起的概率是0.001，即P(B|A) = 0.001，那么当我们看到太阳从西边升起时，我们可以计算出世界即将毁灭的概率P(A|B) = P(B|A)P(A)/P(B) = 0.01，这个公式我们称之为贝叶斯公式。也就是说一件事情发生的概率，会因为一些已经发生的事情而产生改变，当我们判断一件事情发生的概率的时候，需要综合考虑相关的事件。而自回归模型则正是基于这种理念。

来看一个只有两个值的自回归模型：

那这种自回归模型有什么问题呢？

首先，对于高维空间数据，依然不友好，另外作为条件的数据都是同等对待的，但他们其实和要预测的事件也有亲疏远近之分，而在之前的自回归模型中没有体现出来。解决方案有两个，一个是用Reccurent Neuarl Network，一个是Masking。

4. Recurrent Neural Nets （RNN）

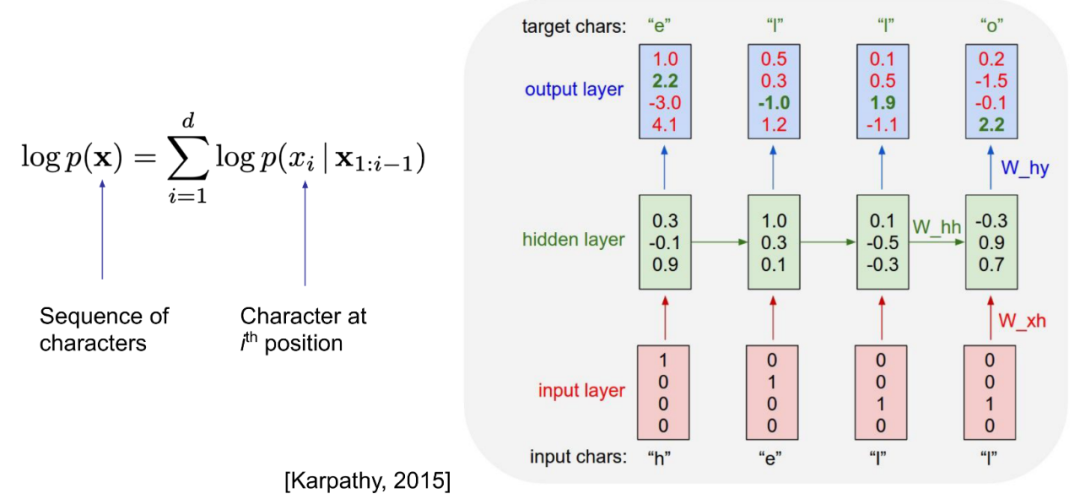
这是上一篇中提到的，在NLP领域十分有效的CHAR-RNN，图右边是一个非常典型的RNN网络。这是一个自回归模型。本质是根据之前出现的字母来推测下一个字母。

RNN在图片生成上的应用，如果单纯根据之前的像素点（像素点依序排列）来推测下一个像素点，可以做到如下效果：

但图像和文字有所不同，文字是一维的，黑白图像是二维的，所以如果依序输入像素点的时候能同时输入每个像素点在图片中的位置，那么训练效果会好很多（很多最先用在NLP领域的模型在被尝试用在CV领域时，都会加入position encoding，典型如VIT）：

5. Masking-based Models

（1）Masked Autoencoder for Distribution Estimation (MADE)

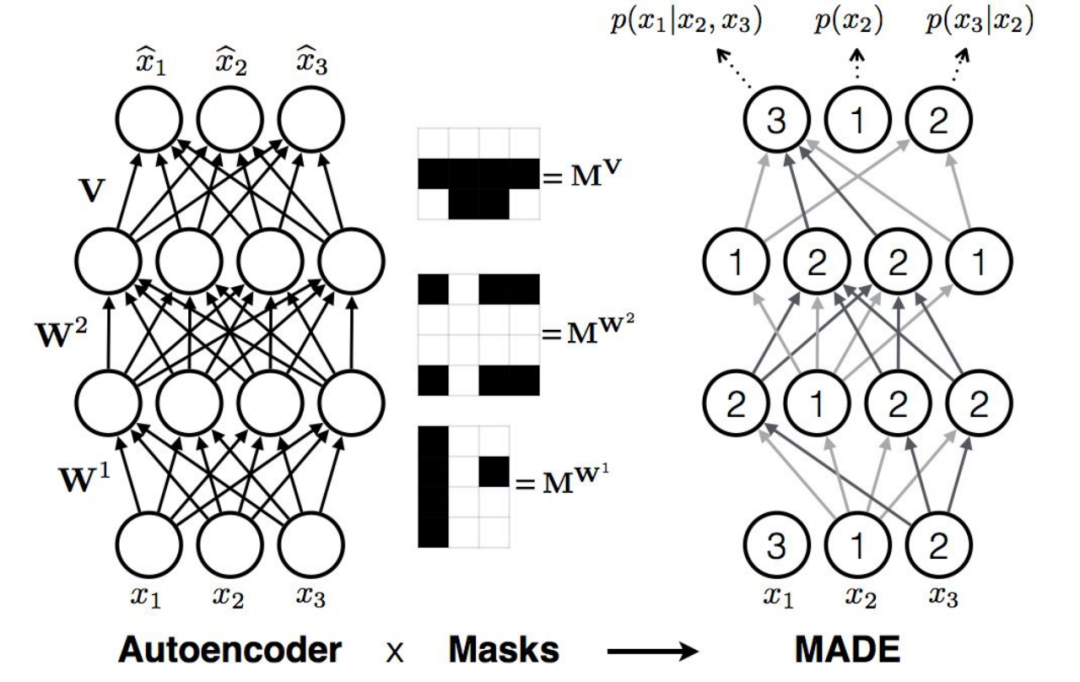
MADE的运作方式就是在一般的aotoencoder上加mask，左边是一个很普通的全连接网络，最后预测出来的每个值和输入的每个值都是相关的，模型会去根据输入样本的所有数据来产生输出，但每层网络加上mask之后，就不一样了，mask不是随机产生的，而是根据需求设计过的，如右边添加了mask后的模型。MADE做自回归模型要输出的和RNN做自回归模型要输出是一致的，都是为了完成下面的计算：

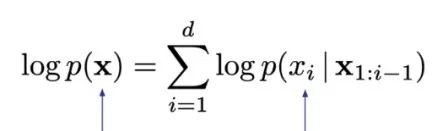
为了实现这样的目标，那么MADE网络最后输出的值，比如上图中网络最后一层的1的输出，它不依赖于任何输入的值，因此它表示一个完全独立的概率分布p(x2)，而2的输出是依赖于x2这个输入的，3的输出则同时依赖于x2，x3的输入，因此可以用来表达条件概率分布。这样MADE就可以获得要用来做自回归的所有概率分布。

这是MADE用于数字生成的效果图，训练集是MNIST。

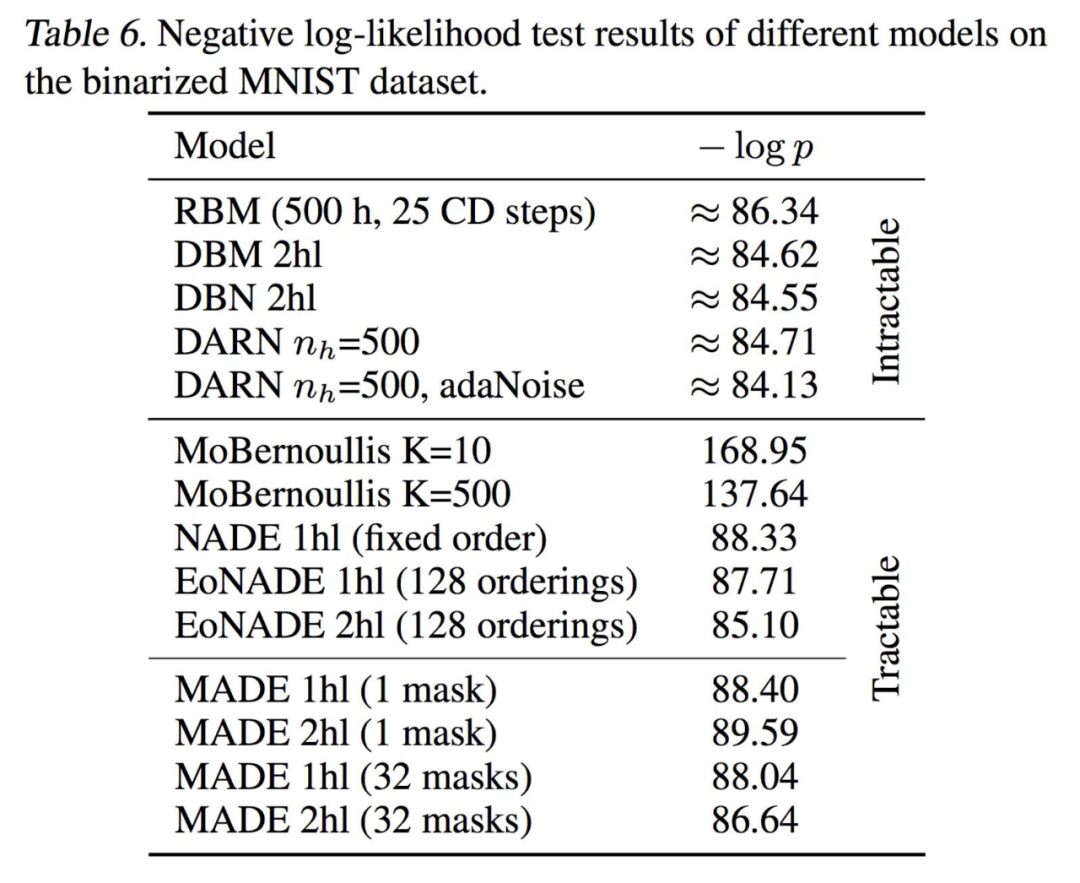
MADE和其他方法的比较。

我们希望MADE具有图像生成的能力，即可以通过训练，学习到特征，从而生成符合预期但却没有过的东西（模型没有见过），而不是直接把看过的图片复制出来，因此研究者会比较生成的图片和训练集中和这些图片最接近的图片。如果完全一致，模型其实只是记忆和复刻了训练集，而如果是特征一致，但细节不一致，就说明有生成的能力。上图左边是模型生成的图片，右边是和生成的图片最接近的训练集中的图片，发现大多数其实是特征一致，但是细节不一致，所以我们可以初步得到结论，MADE具有生成的能力。

自回归模型图片中数据输入是有一个顺序的，那么怎么给一个图片中的数据排个序，怎么排序才能使模型有更好的生成能力，这也是一个问题。上图中尝试了不同的像素排序方式，比如完全随机，比如先单数后双数，比如一行一行扫描，一列一列扫描等，效果大家自己观察了，PPT上的这个图和视频课程里的这个图出入有点大。

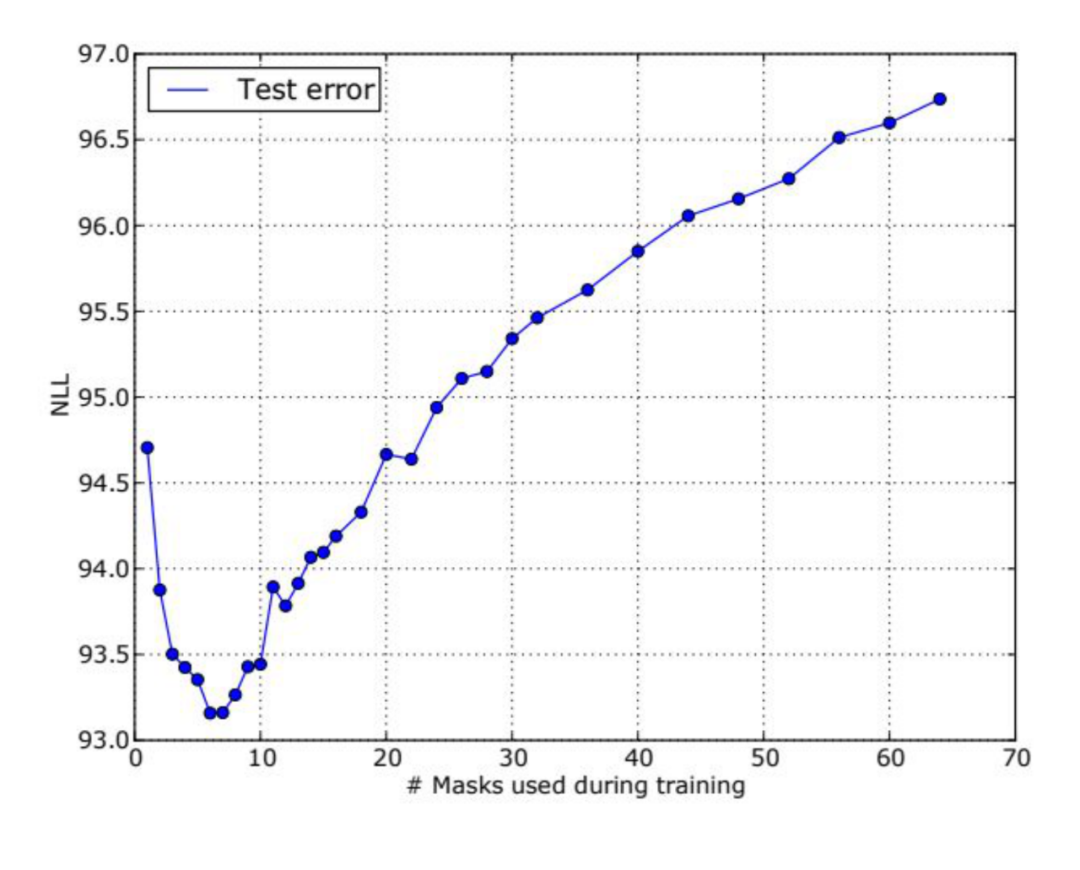
Mask的数量和训练效果的关系，如上。不过值得注意的是，因为训练的是生成网络，所以模型的优劣有时候不太能直接用这种硬指标来衡量。

视频课程也有描述怎么用训练好的模型sample，这里基于一开始的那张图简单说一下，x1可空，然后产生p(x2)，根据p(x2)确定x2的值，作为输入，输出p(x3|x2)，根据p(x3|x2)确定x3的值，再输入x3，再跑模型得到p(x1|x2,x3)，以此确定x1的值。可以发现，这个模型在sample的时候其实很像RNN，比如上面生成数字图的任务，要一个一个像素生成，要生成一张（28，28）大小的二值图，需要把这个模型跑784次。

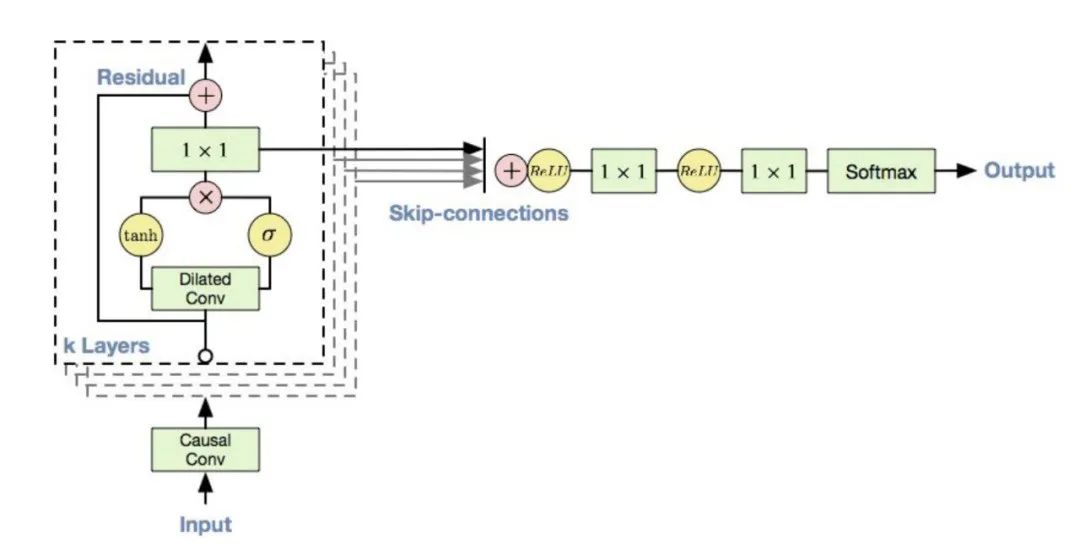
（2）Wavenet [Masked Temporal (1D) Convolution]

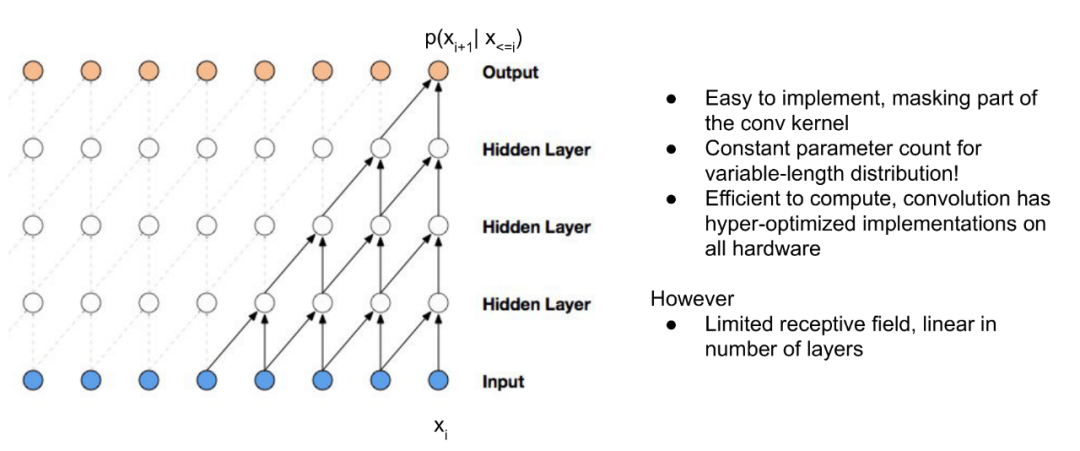
上图就是一个简单的Wavenet网络，每一层都有一个一维的长度为2的卷积核，步长为1。这个方法的优点是容易实现，不论输入有多长，参数量没有变化。缺点是计算出的概率分布，能观察到的输入是固定的，比如上图中，虽然输出是p(xi+1|x<=i)，但实际上计算的分布是p(xi+1|x（i-4) - i)，如果想要p(xi+1|x<=i)，那么还是需要调整输入的大小，或者重新训练匹配输入大小的网络。当然也可以有其他解决方式，比如下面这个网络，用了Dilated Conv。

这是Wavenet的生成效果。

这是加入position encoding之后，Wavenet的生成效果。

（3）PixelCNN [Masked Spatial (2D) Convolution]

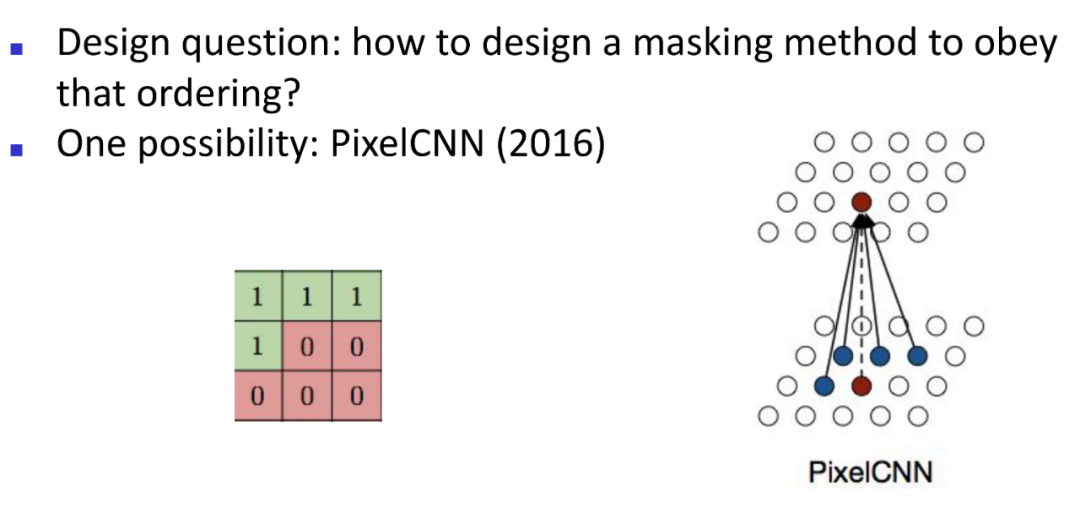
上面的方法都是一维的方式加上position encoding来完成图像生成，那么当然就有人会尝试二维卷积的方式来做这件事情。PixelCNN是2016年的时候被提出来的一个网络结构，这个网络依然是一个像素点一个像素点依序生成，如上图所示，现在想要生成右图中红色那个位置的像素值，如果用一个3*3的卷积核，那么会被参考的像素值是它周边的四个已经生成的像素值（蓝色位置），其他五个不参考是因为他们还没有被生成出来。这是一层，一般会有多层。这里先看一个Sample的效果，是一个一个像素点生成的：

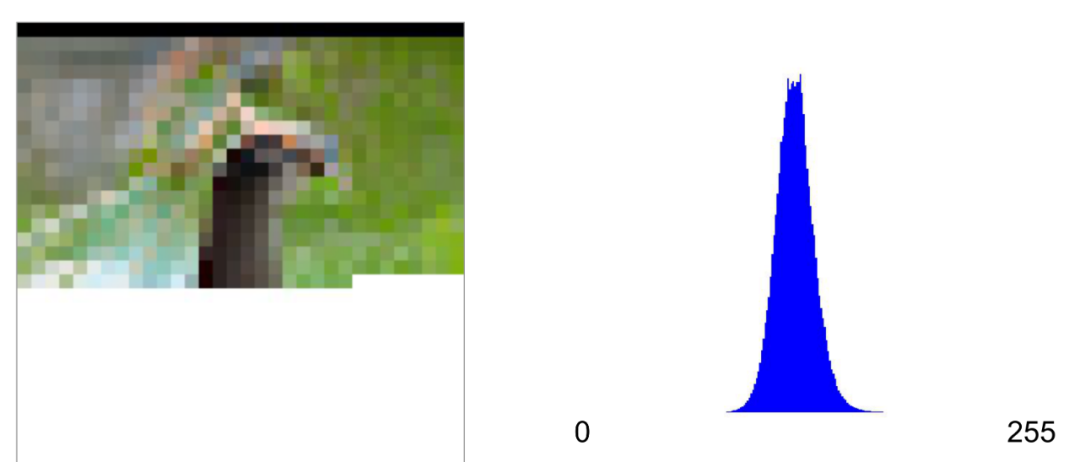
如上图所示，已经生成的图片如左图所示，左边是输入，而输出是一个概率分布，如果像素值的区间是[0,255]，那么就是该点像素值在0到255区间的概率分布，如果是二值图，那么横坐标只有两个值，0和1，输出就是像素值在[0,1]区间的概率分布。像素值是离散值。如果是彩色图，输出应该是三个概率分布。

（3）Gated PixelCNN

如果PixelCNN网络有不同层数，那么会被参考的像素值如下图[1]所示：

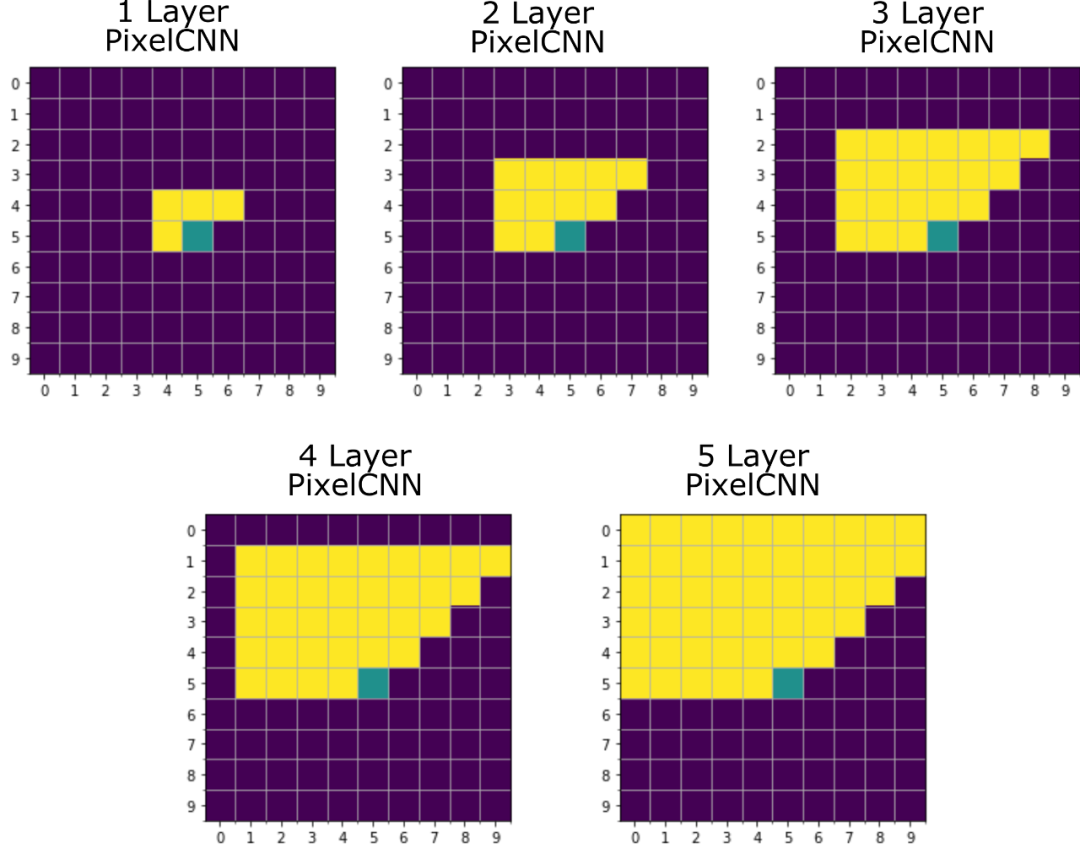
按现在的结构，网络层数越多，生成这个像素值会参考到的范围越大，但是会发现，因为卷积核本身的结构特质，会有同样也很近的像素值，没有被平等地参考。应该但是没有被参考的部分被称之为Blind spot。

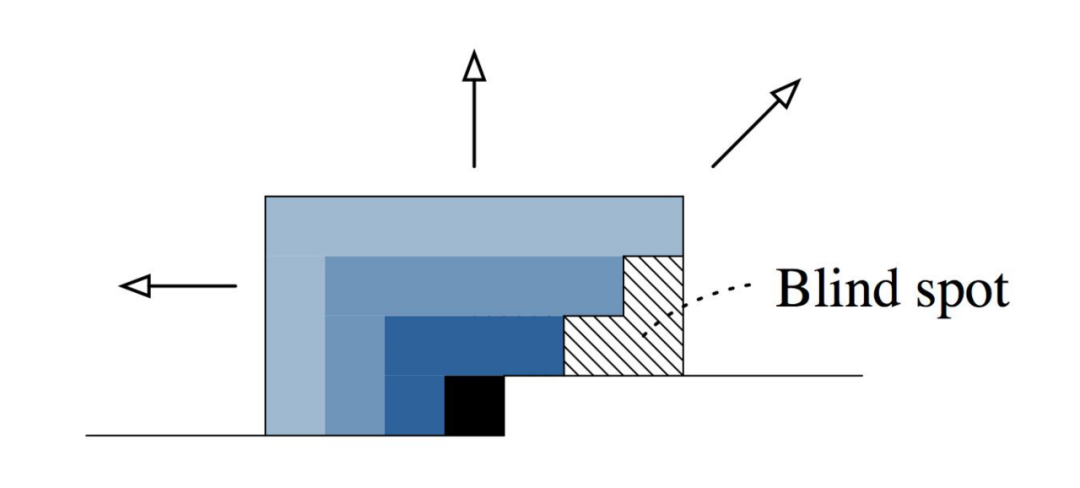
为了解决这个问题，Gated PixelCNN被提了出来（图来自参考[1]）：

为了规避Blind Spot，这里设计了两个卷积核，一个是上图中绿色部分，中心点是m，m是要生成的r的正上方的位置。卷积核是33大小，但是最后一行是0，这样不管网络有多少层，右边都不会再出现Blind Spot。但这样会忽略掉左边的已经生成的像素值，因此还有一个卷积核是13，只是右边两个值是0。不同层数的Gated PixelCNN参考的像素值范围如下图[1]所示：

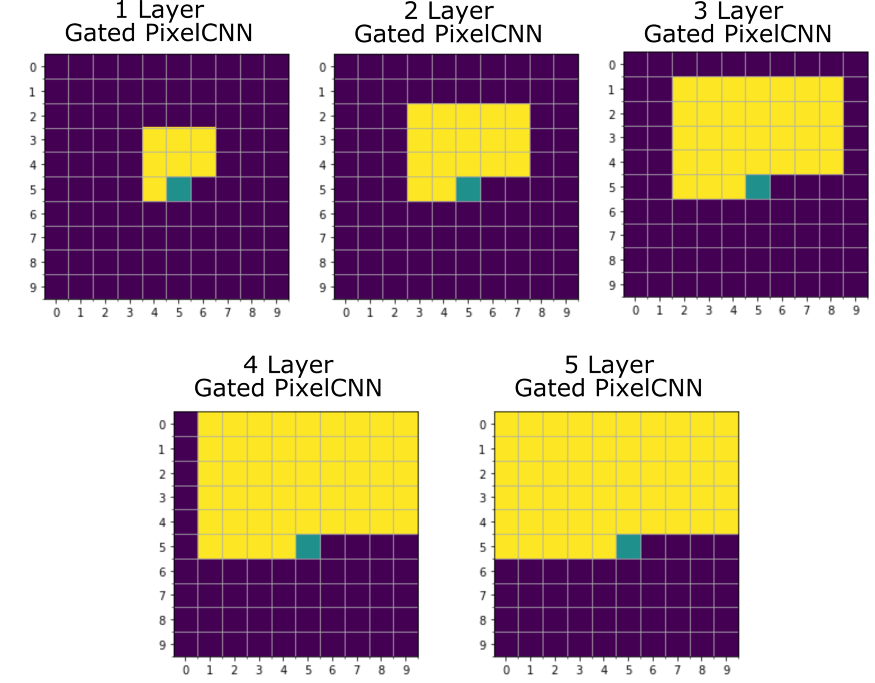
这样就没有Blind Spot了。

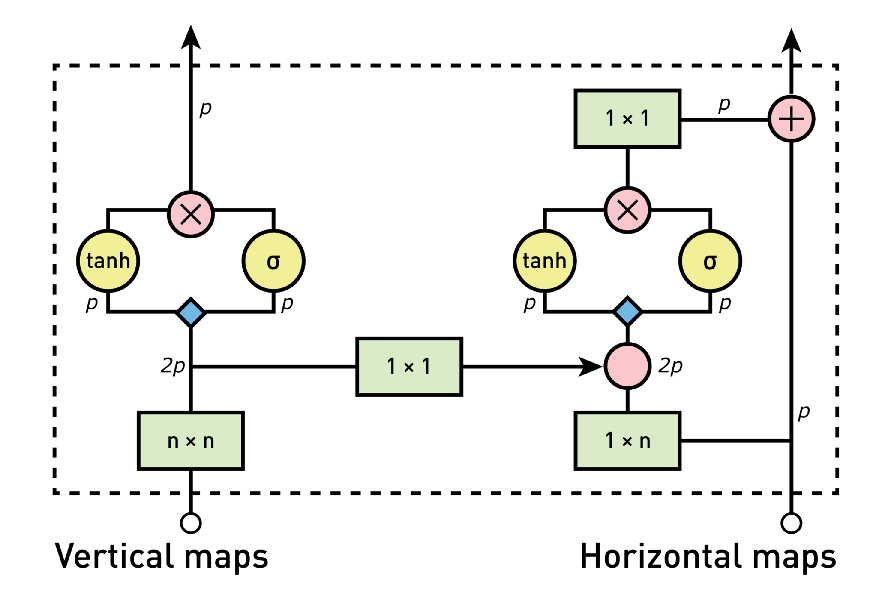
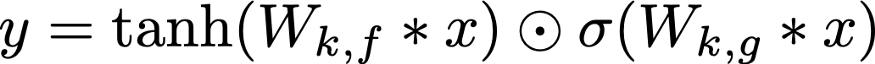
Gated PixelCNN网络架构如上图所示。之所以这个网络前面加了Gated字眼，不是因为卷积核的变化，而是网络结构中加入了类似LSTM中记忆门（forget gate）的机制，上图中tanh函数生成的是概率分布值，而σ生成的是遗忘值，决定tanh生成的概率分布该如何保留。

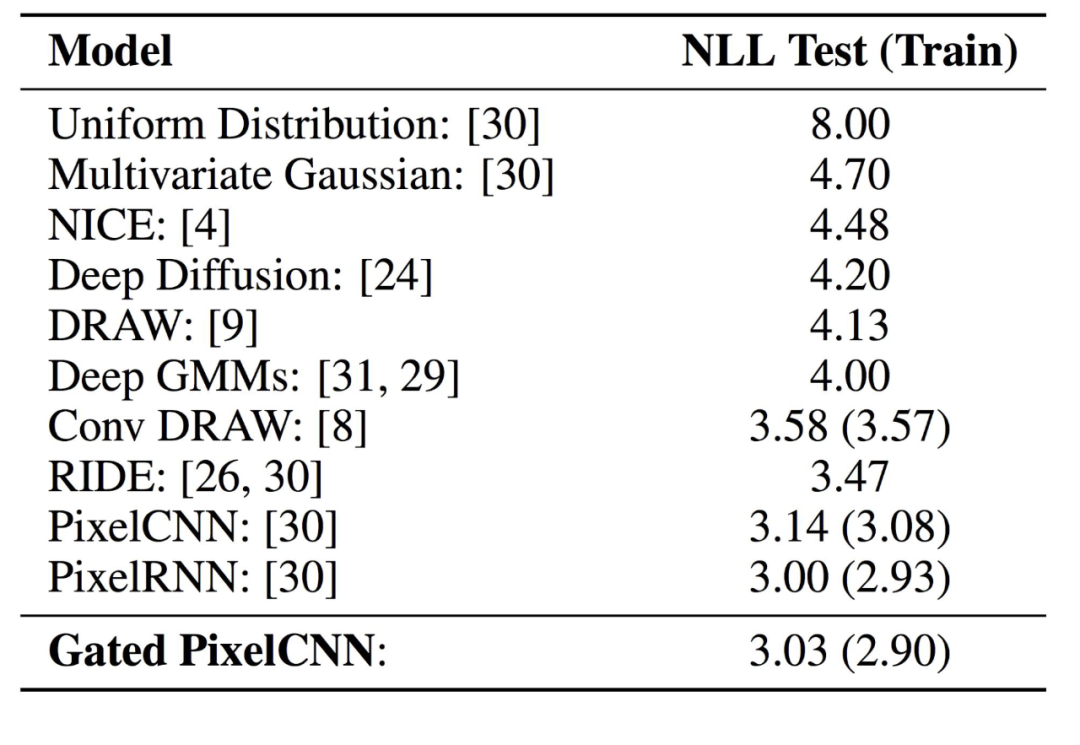
上图是一些方法的比较。

（4）PixelCNN++

PixelCNN或者Gated PixelCNN每次输出的是一个分布，如果是彩色图，输出的是三个在[0, 255]区间上的概率分布。这存在的问题是，首先，输出的量大，计算量也就大，另外一个问题是这个像素是254的概率和这个像素是255的概率其实是强相关的，但这种方法有点像在解两个问题。因此PixelCNN++做了改变。

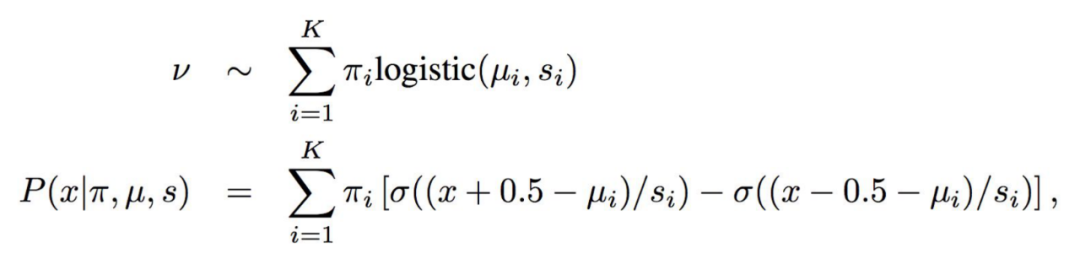
本质上是把一个求离散概率分布的问题变成了求连续概率分布的问题，如上面两个公式，最后得到的不是一个概率分布，而是一个概率分布函数，u决定了这个函数的位置，s决定了这个分布的形状，如下图所示：

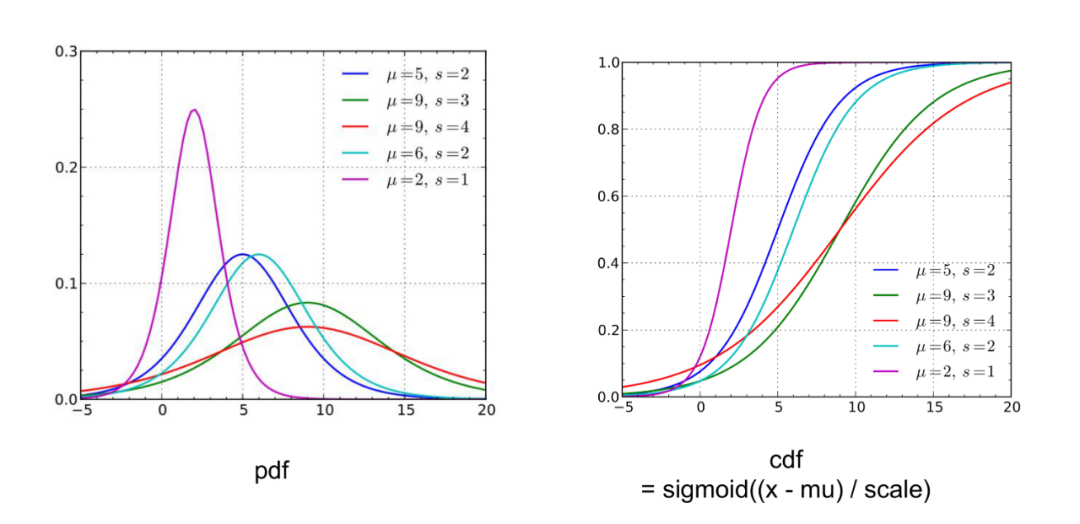
PixelCNN++还在通道上做了改进，PixelCNN或者Gated PixelCNN是分别输出三个概率分布，但颜色之间也是有相关性的，PixelCNN++则同时参考了不同颜色，输出的也是联合概率分布。

PixelCNN或者Gated  PixelCNN无法依赖远距信息，因此PixelCNN++为每一层添加了一个下采样，这样虽然损失了信息，但是扩大了生成像素可以参考的范围，而损失的信息可以用额外的方式来补偿，如下图所示：

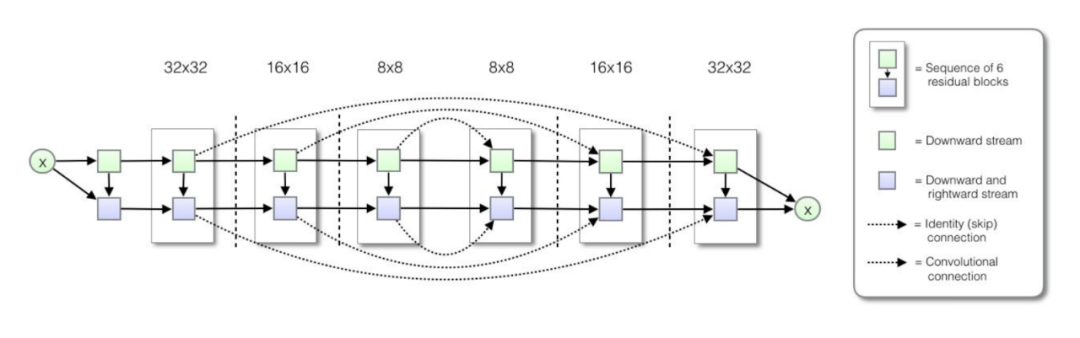
模型的测试结果如下：

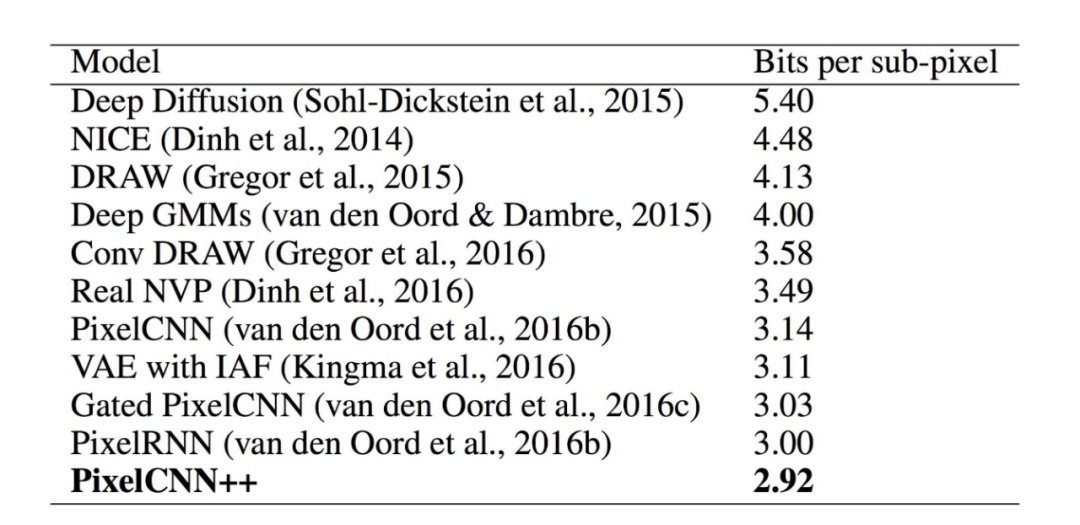
更详细可以参考[2]或者看原paper。

（5）PixelSNAIL

还有融入了残差模块和注意力机制的PixelSNAIL，这部分课程讲的不太清楚，但提出这个网络的有公布论文和代码。这里就简单描述一下这个网络，主要是融入了attention机制：

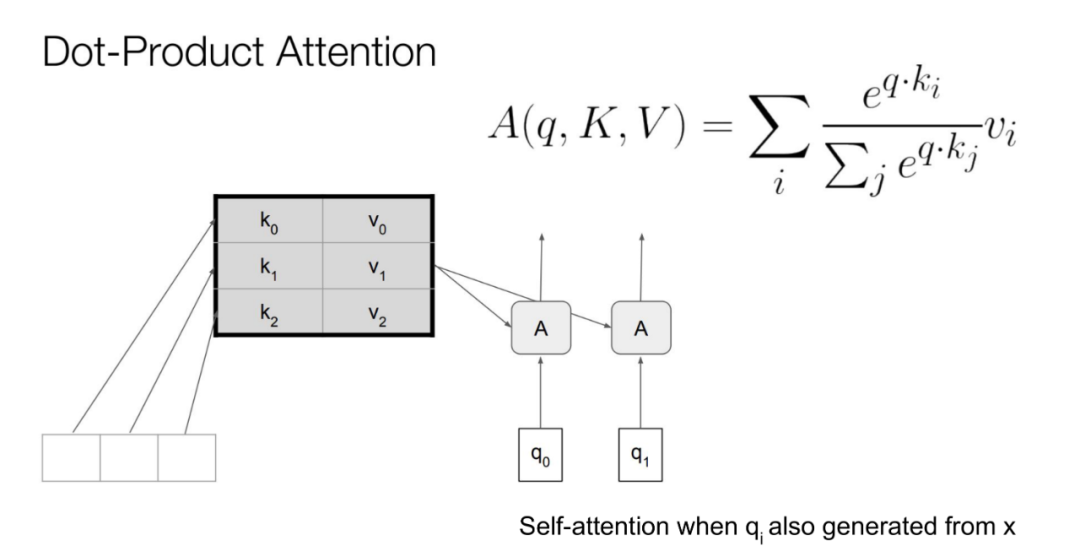
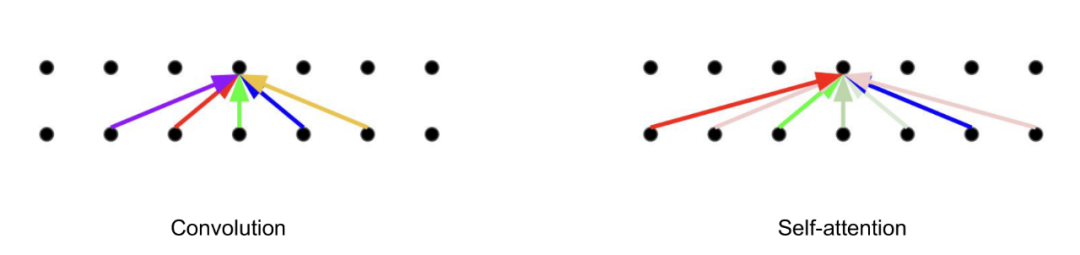
卷积让网络只能参考到一部分信息，但是attention可以参考所有信息。

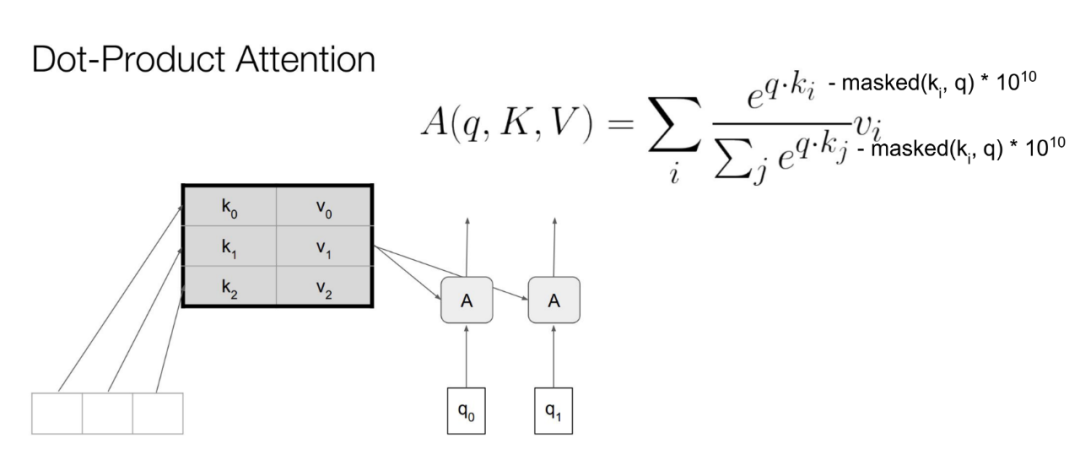
进一步说，应该是masked-attention。这种机制让这个模型相较于其他模型，在生成一个像素值的时候，几乎可以参考之前已经生成的所有像素值。

这种方法可以允许模型用不同的顺序生成图片，比如上面这种顺序。

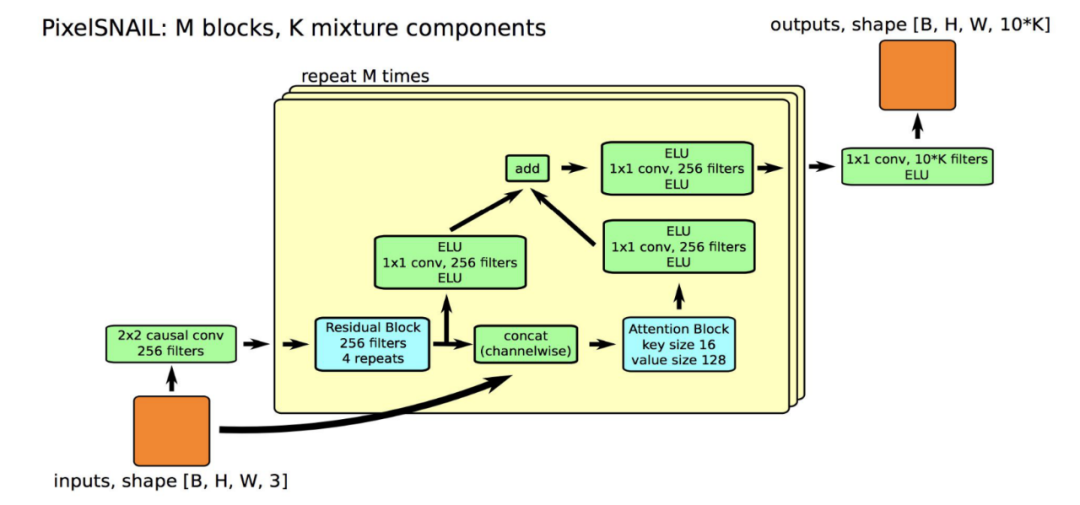
网络的核心就是一个Residual Block和一个Attention Block。

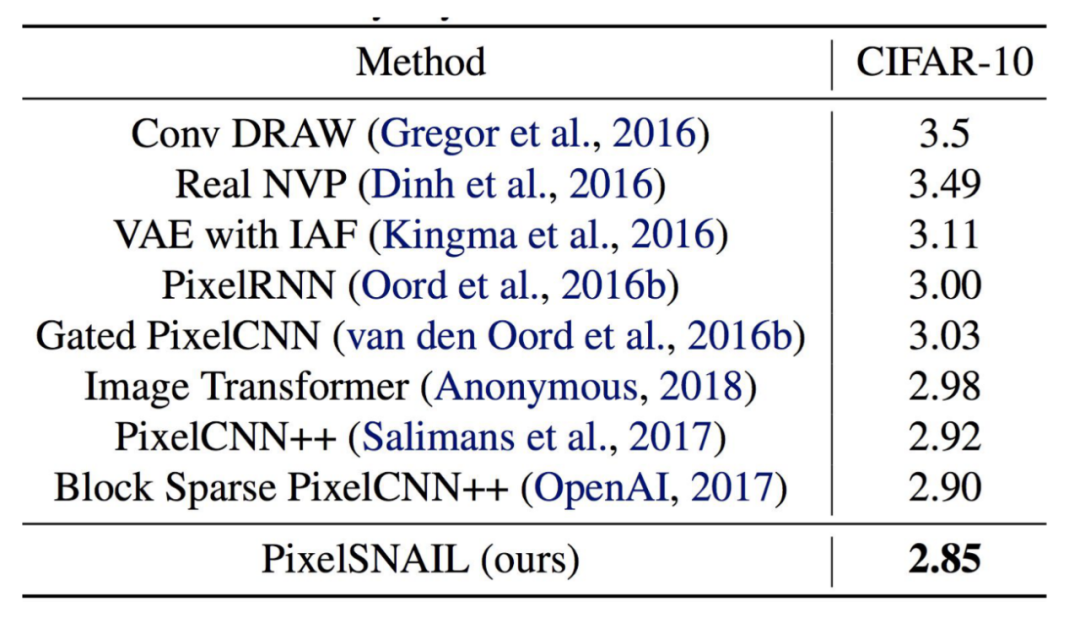
他的效果超越了之前的模型：

（5）其他

1. Class-Conditional PixelCNN 可以指定数字生成。
2. Hierarchical Autoregressive Models with Auxiliary Decoders可以生成真实到肉眼无法分辨的图片。

1. PixelCNN可以用来提高图片清晰度

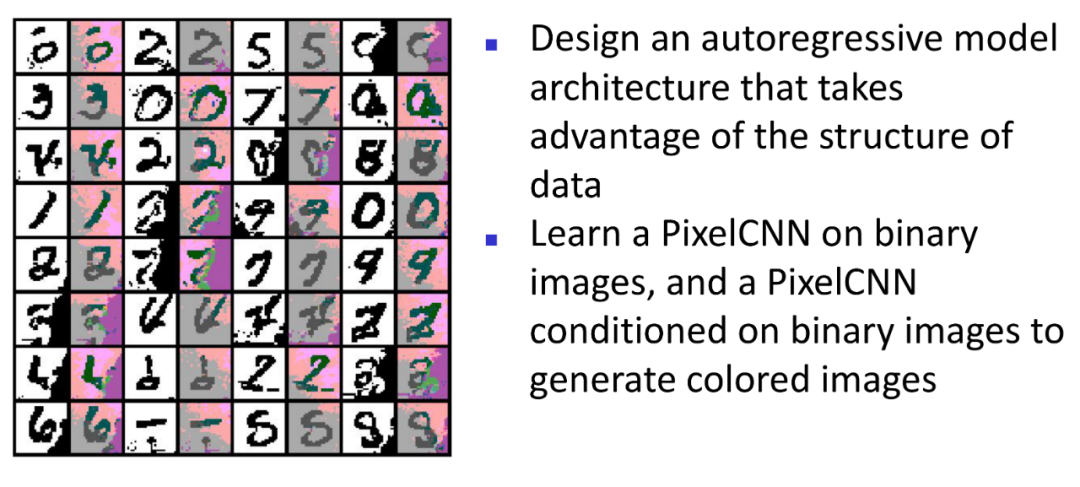
4. PixelCNN可以用来黑白转彩

1. PixelCNN一个一个像素点生成有点慢？可以加速

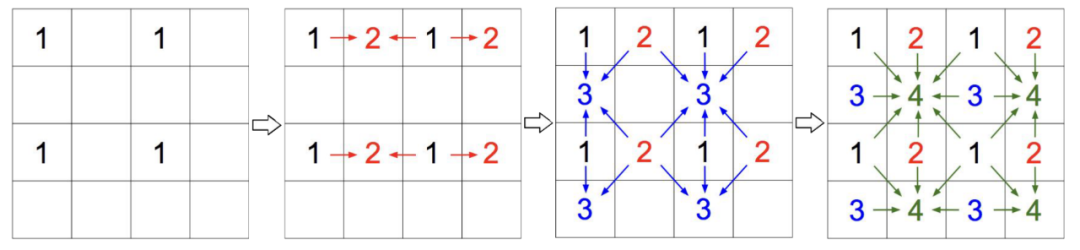
分块加速，比如把图片分成四块，如上图所示的方法加速。

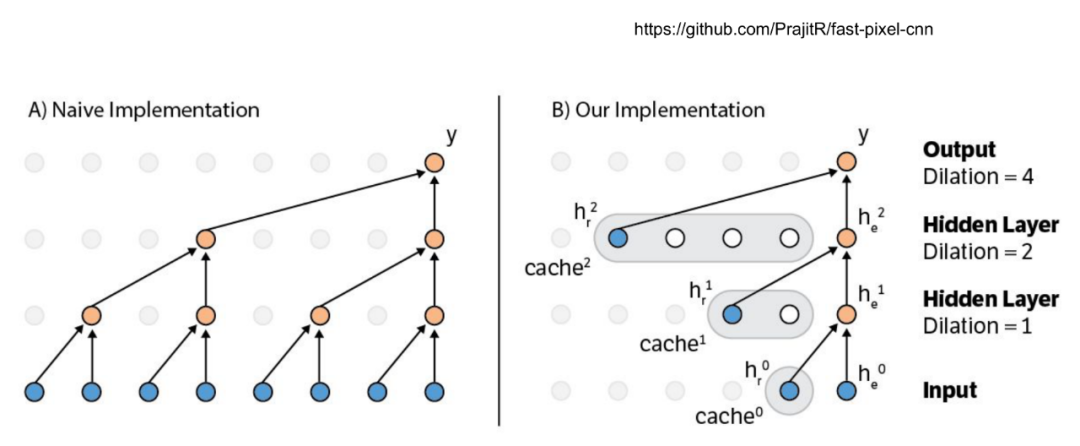
也可以尝试其他技术加速，比如cache activations。

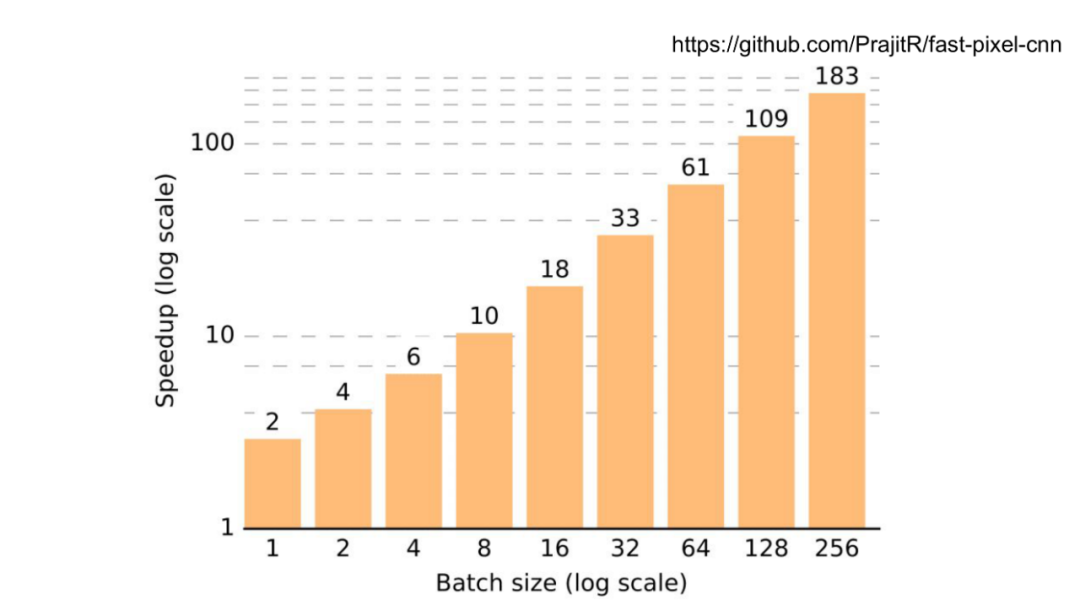
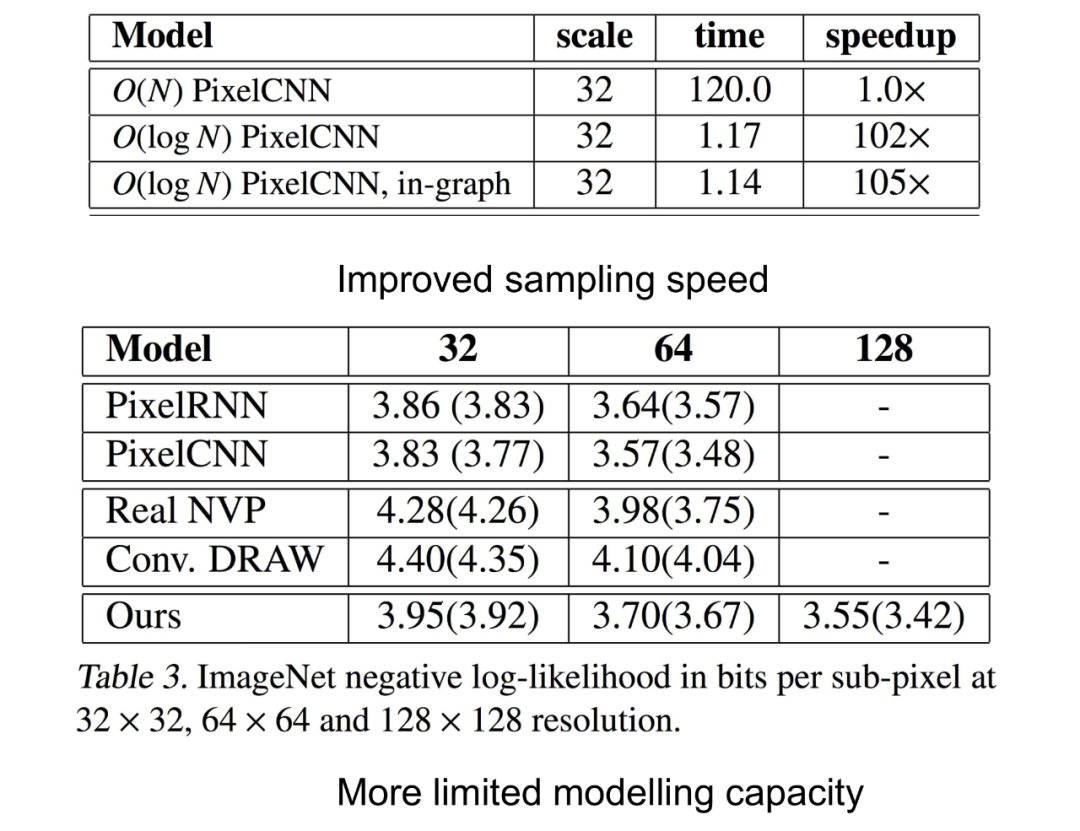
以上是加速效果。

1. 也可以做视频生成

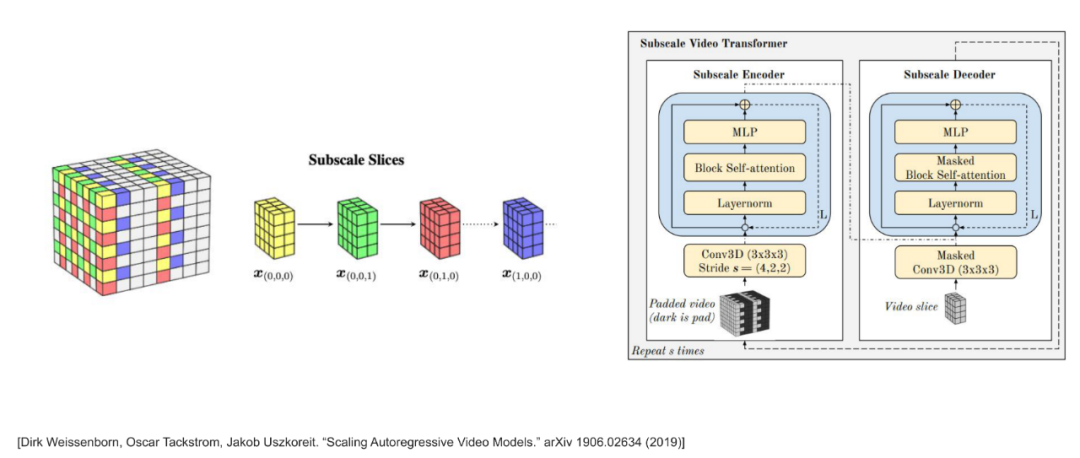
1. 也可以做人脸生成

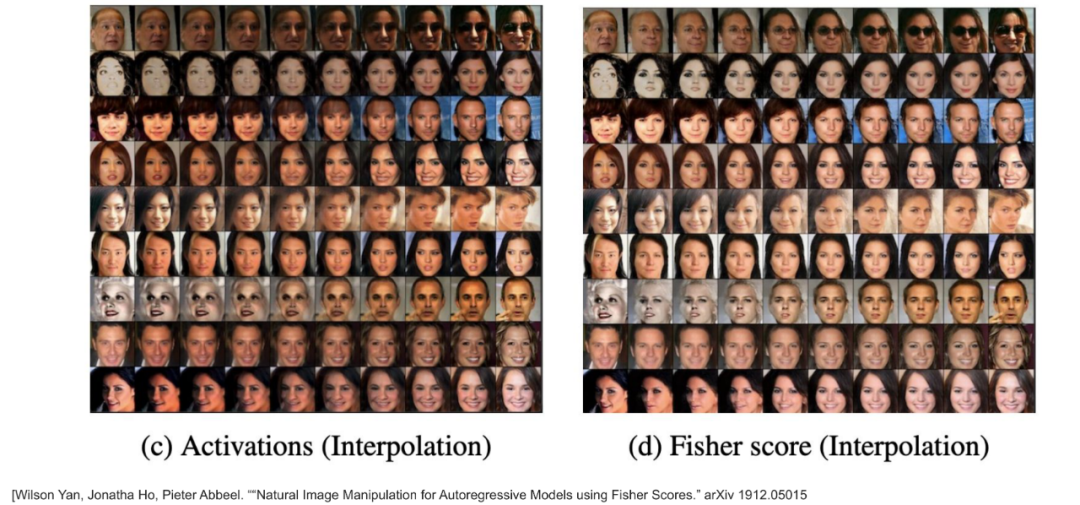
PixelCNN因为是一个像素一个像素输入，一个概率分布一个概率分布输出，所以我们很难得到一个特征向量来代表一个人脸。然后通过改变特征向量来生成不同的人脸。加入了Fisher Score，自回归模型也能很好的做一张脸到另一张脸的转换，如上图所示，左边做人脸的变化，出来的效果像是把两张人脸叠起来，先让一张脸显现，弱化另外一张脸，再逐渐让另外一张脸显现，但右边的图不一样，从一张脸到另外一张脸的变化中，产生的都是真实度高的不同的人脸。

下面一行用了Fisher Score的方法，可以发现，比起上面那行，下面这行在慢慢变化的过程中，产生的都是真实度高的人脸。

声明：以上所有图片和技术内容，均来自UC Berkeley非监督学习课程和参考文章，没有原创理论和图片。

参考：

[1] Jessica Dafflon,  PixelCNN’s Blind Spot, towards data science, 2019

[2] Harshit Sharma, Auto-Regressive Generative Models (PixelRNN, PixelCNN++), 2017