一、因果关系的意义
看下面这两张图：
<div align=center>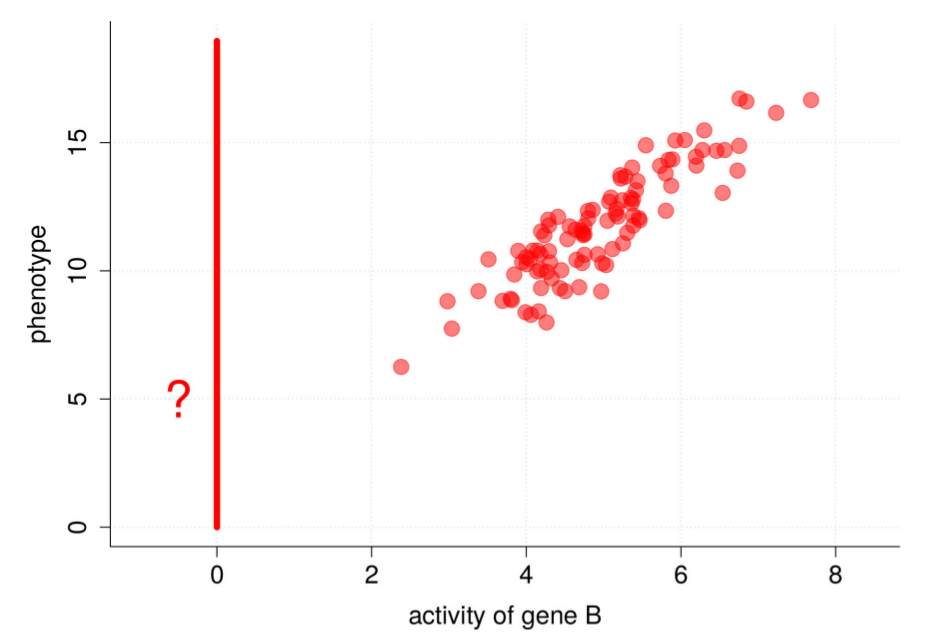
</div>
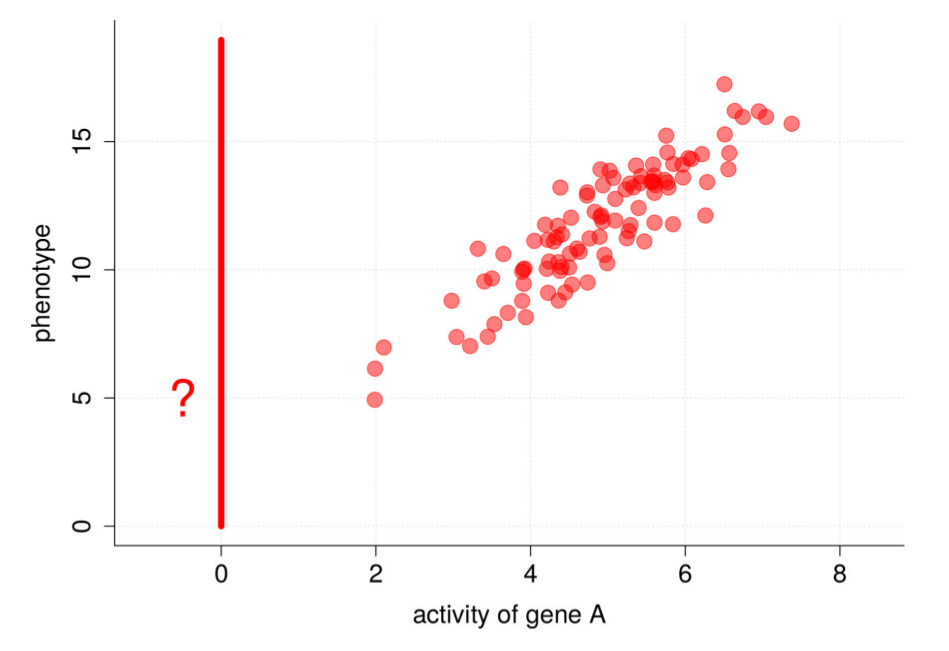
两张图分别是基因A, B活跃度变化的时候，phentype的变化，那么现在我们来思考一个问题，如果我们把基因A或B单独删掉，抑制其活跃性，那么phenotype的值会落在哪个区间?
看删掉基因A的结果:
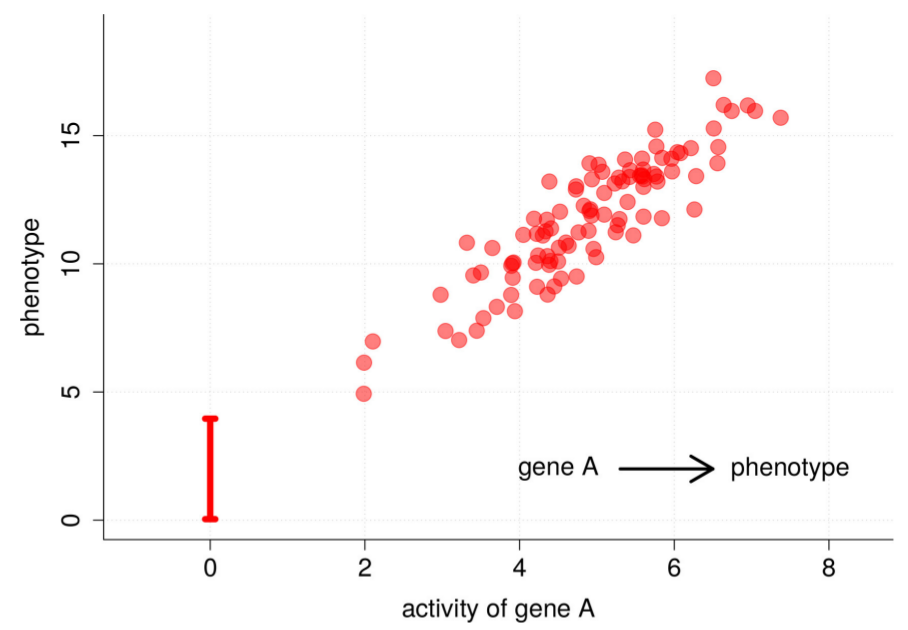
如果删掉基因A，phenotype的值会降到红色线条所示的区间，因为A的活跃度影响着phenotype的值，两个元素之间成因果关系。
再看删掉基因B的结果：
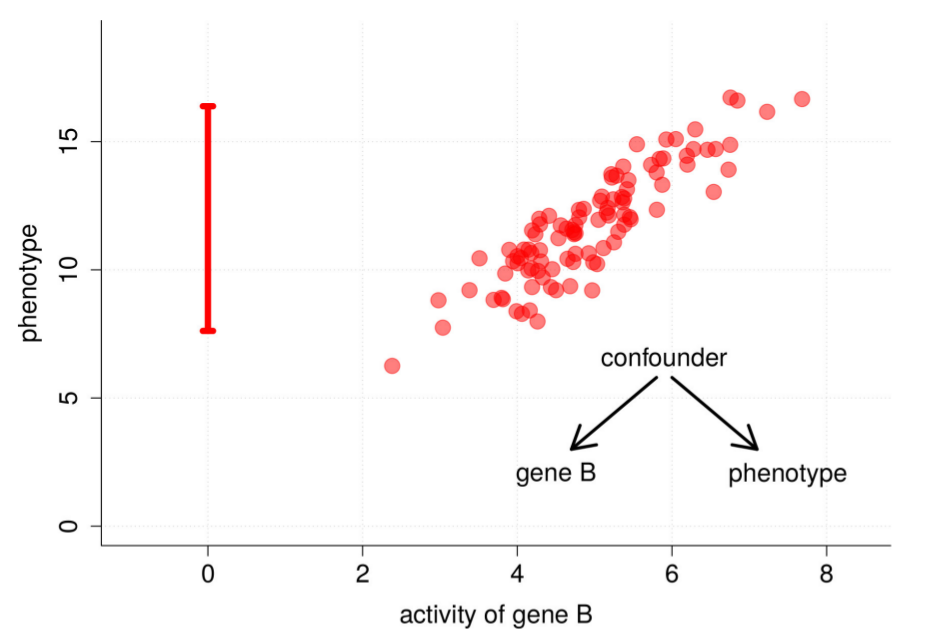
如果删掉基因B，phenotype的值还在原来的区间，没有产生明显的变化，因为基因B和phenotype同时被另一个元素confounder影响，它们之间本身不构成因果关系，只是单纯的相关关系。
通过上面的示例，可以大概了解到，通常我们都在研究相关关系，而因果关系是不同的，检验是因果还是相关，可能需要主动干预，形成对照。
毫无疑问，因果关系的确立有助于我们判断事物的发展。
二、因果模型
因果模型是什么？
<div align=center>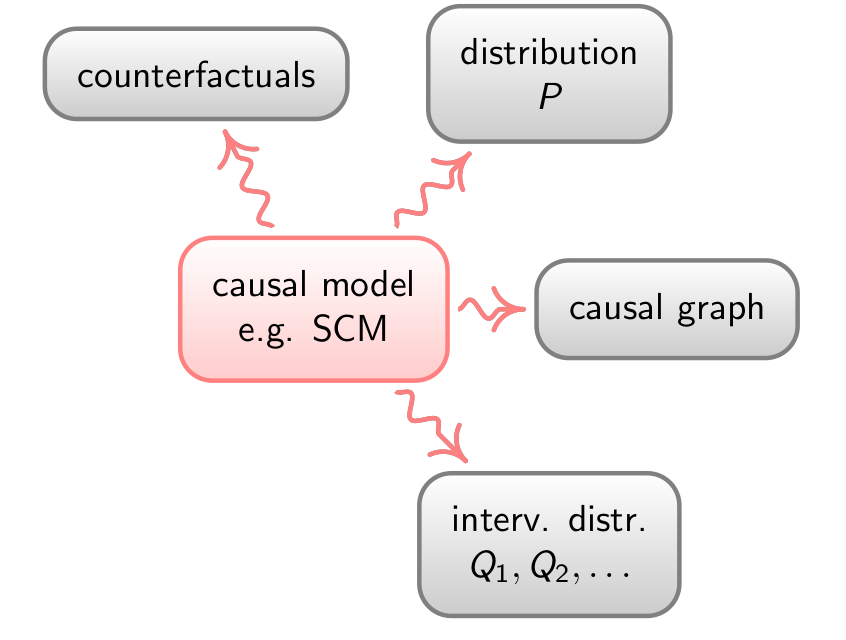
</div>
以结构化因果模型（Structral Causal Models, SCMs）为例，因果模型应该包含如上图所示的四个部分：
1. Distribution，SCMs要能解释数据的分布状况 2. Causal Graph，生成可以表现因果关系，因果结构的因果图 3. Intervention Distribution，模型能预测干预后系统的反馈 4. Counterfactuals，模型可以做反事实推断
这里比较难解释的是反事实推断，第一个部分是现在的机器学习和深度学习方法可以轻易实现的，即挖掘数据和数据，数据和概念等等之间的相关性，比如人类拥有的感知外界的功能，看见一只鸟，传入眼睛的是光折射出的图案，但人有能力将这个图案和鸟这个概念关联起来，现在计算机也可以。第三个部分是干预，即人类偶尔知道做什么样的行为，可能能得到自己想要的结果，比如他看见一只鸟，他知道如果他想吃到鸟肉，他得把这只鸟打下来，要把这只鸟打下来，他得有弓箭，猎枪或者其他杀伤性武器。第四部分则是反事实推断的能力，即能够做如果…，那么…的假设和推断，“如果那天我没有把那只鸟打下来，吃上肉，我现在还活着吗？”，“如果当时那只鸟飞得再高一点，我还能打到它吗？”，这对应的是人类想象，回顾和理解的能力。关于这部分概念，可以参考《The Book of Why》的第一章和第八章。
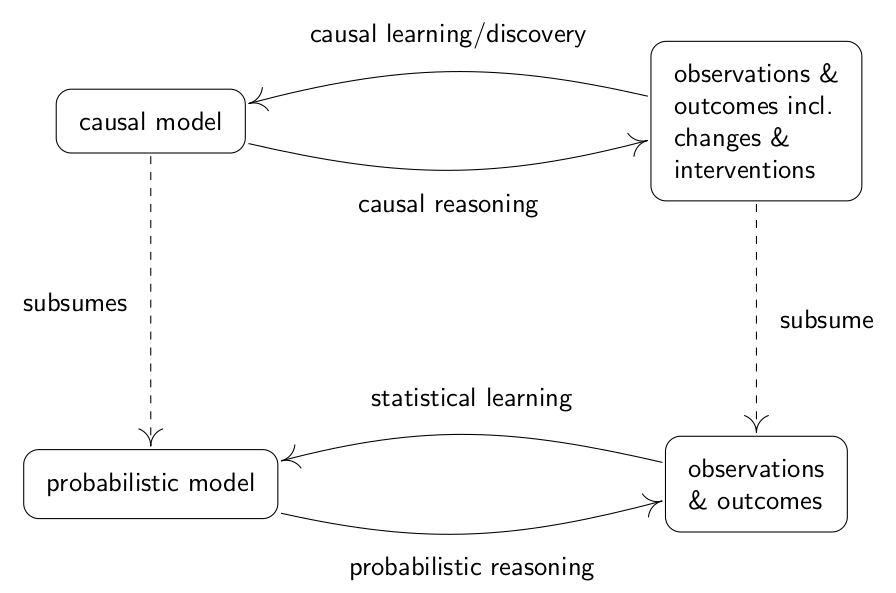
接下来看因果推理和因果学习的概念，上图是因果学习和推理对照概率模型的示意图，如概率模型一样，如果有了模型，那么就可以根据观察到的数据进行推理，如果有完整的观察到的数据和数据对应的结果，则可以进行模型训练，学习。但因果学习和概率模型的学习有很不一样的地方，假设你有无限多的数据，即你知道每一种可能和其对应的答案，那么训练概率模型就没有必要了，而因果模型却还是要经过学习，发现的过程才能得到。
三、因果关系相关的案例
1. 巧克力和诺贝尔奖
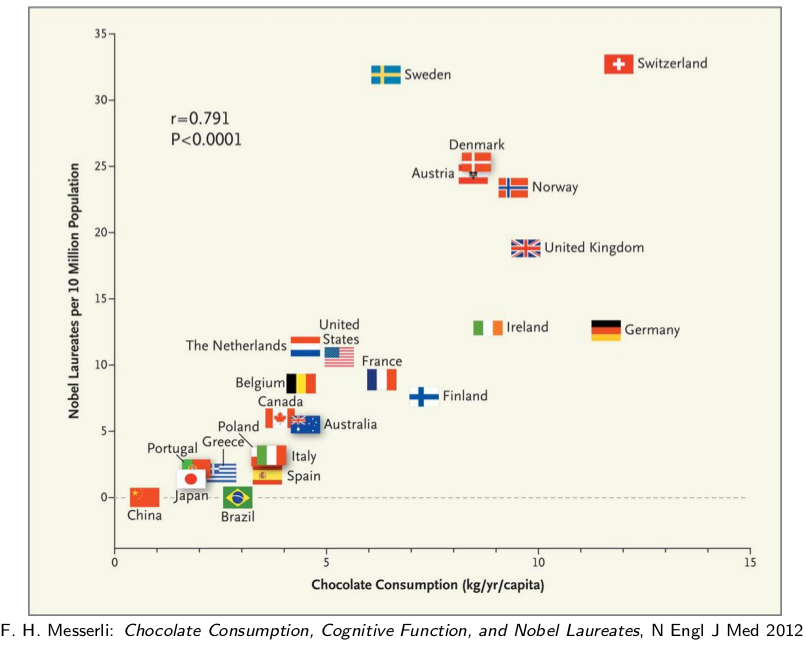
上面这幅图中，横坐标是人均每年吃的巧克力的量，纵坐标则是每千万人中获得诺贝尔奖的数量。根据上面的图，可以轻易的得出结论，巧克力的消耗量和诺贝尔奖的获奖数量是强相关的。因此就有了下面的一些报道：
吃巧克力，可以增加获诺贝尔奖的人数，以及下面这则新闻，聪明的人似乎更爱吃巧克力。
这是一个典型把相关性当成因果关系的案例。
2. 抽烟和肝癌
上面这篇发表于1950年的文章，证明了吸烟和肝癌之间存在强相关性：
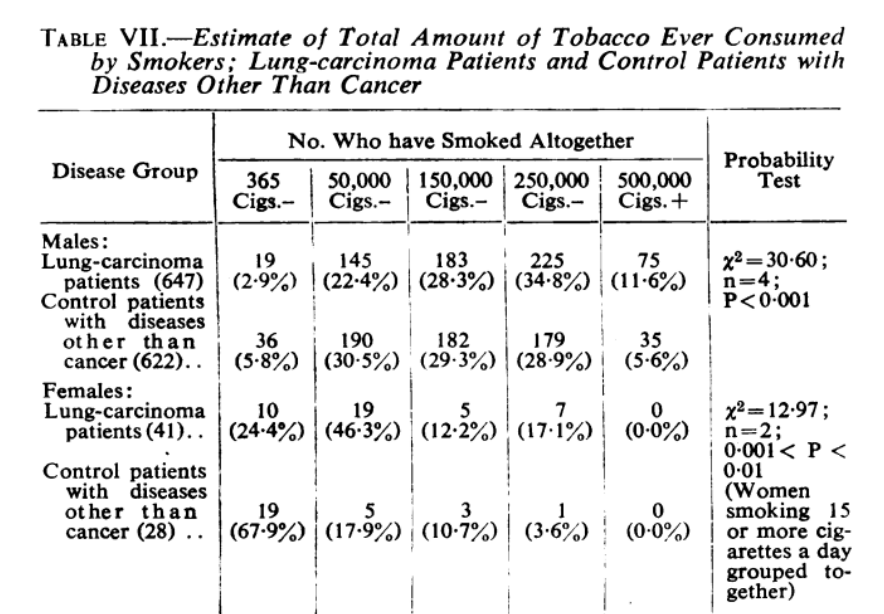
所以政府想说，哎呀，吸烟导致肝癌啊，那推出烟草税吧，烟草公司就不乐意了，站出来说，并不一定是吸烟导致了肝癌，或者提高了得肝癌的几率，也有可能是一个不知名的原因，共同导致了抽烟过多和肝癌呢？
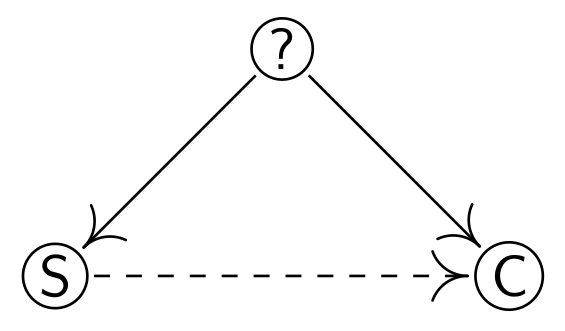
怎么判断抽烟和肝癌之间存在因果关系，还是它们两个有一个共同的原因导致，是关键的问题。
3. 夜间光照与近视
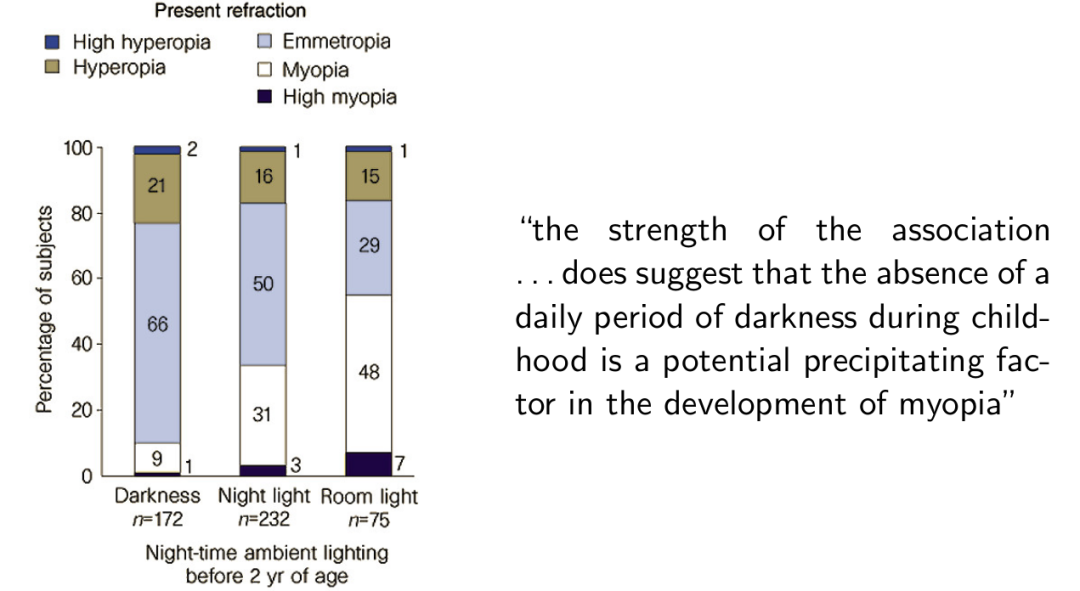
左边这幅图出自一个关于近视的研究，这个研究表明，被家长更多地提供夜间照明的孩子们反而更多的患上了近视。也就是夜间照明和近视强相关，夜间照明极有可能是近视的一个诱因。
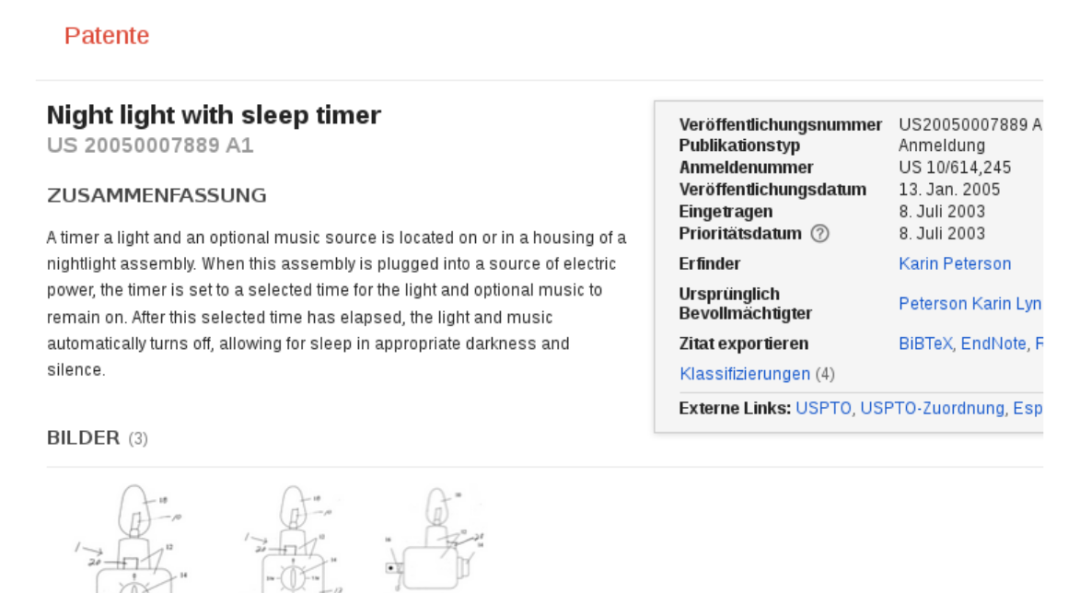
因此，有专利就把夜间照明和近视当成因果关系，做了发明。但它们其实不算是因果关系，只是有可能是因果关系。
4. 肾结石的两个治疗方案
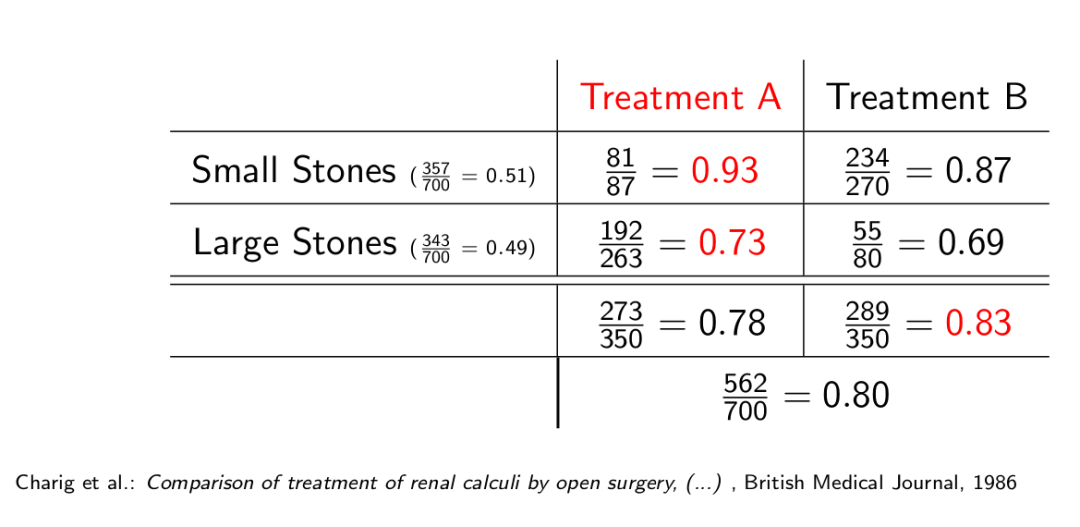
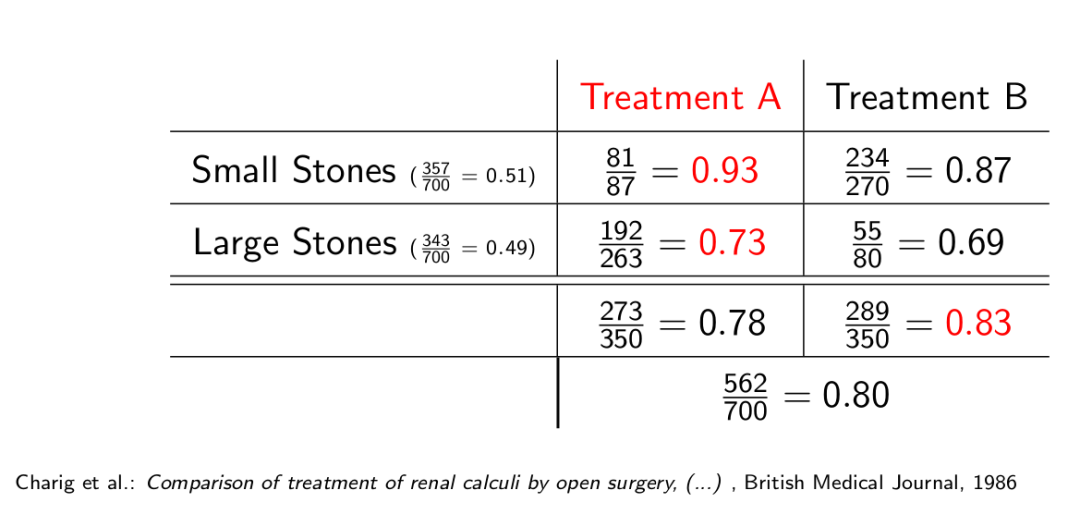
肾结石有两个治疗方案，A和B，如果看总的治愈率会发现，B方案明显好于A方案。但是肾结石的石头又可分为大小两种情况，从这两种情况的治愈率来看，A方案又明显好于B方案，造成这种结果的原因是，治愈率不但和治疗方案有关，还和结石大小有关，A方案的治愈率虽然高，但主要用在了治愈率较低的大结石这种情况，而B方案则主要用在了治愈率较高的小结石这种情况，因此，简单地比较总的治愈率，对A方案来说是不公平的。治愈率，结石大小，和治疗方案的因果关系可以以下图表示：
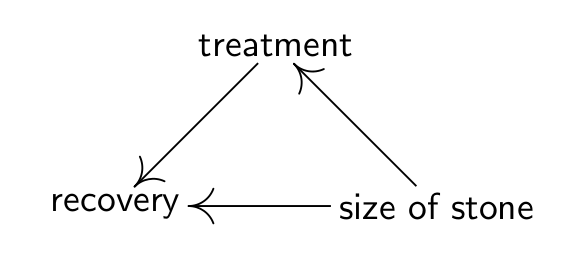
5. 广告推荐
当我们使用搜索引擎搜索一些东西的时候，或者做一些其他和网络互动的时候，经常会被推送一些广告，如下图：
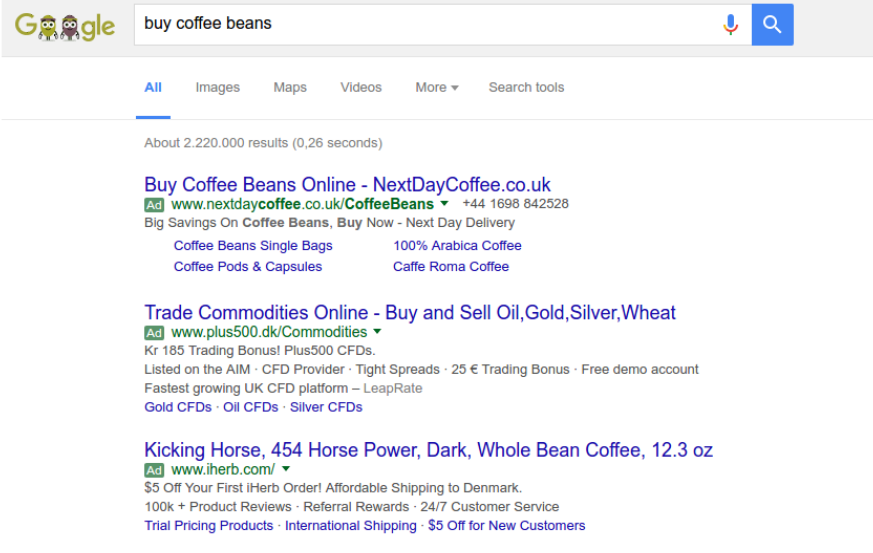
下面这个研究则通过研究推送广告过程中的因果关系来优化模型：
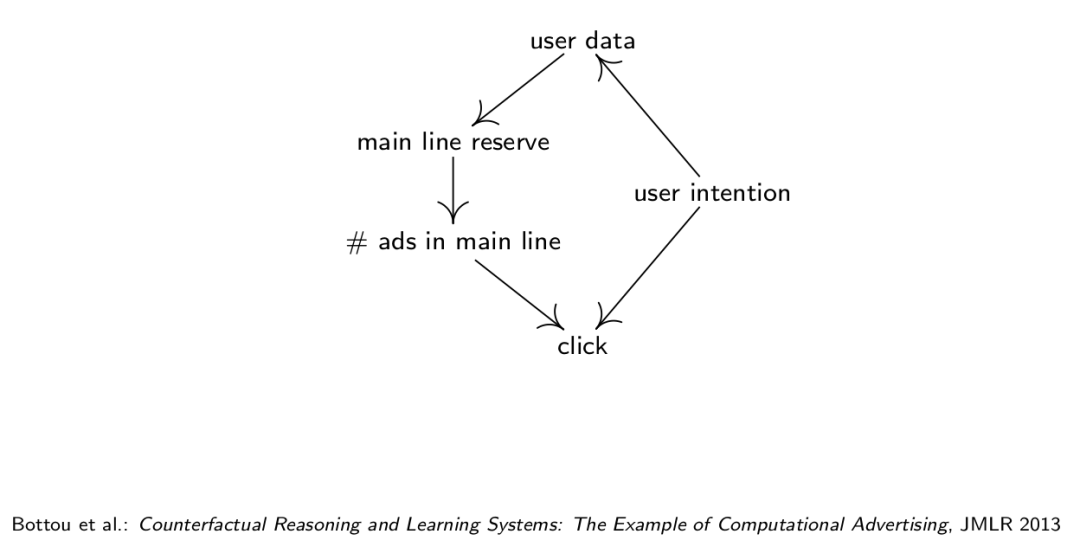
用户的意图会决定用户的操作和一些其他的数据，而通过分析用户的数据，我们来决定给他推送什么样的广告，以及推送多少广告，而这些又会一定程度上决定用户的行为。
6. 基因的相互作用
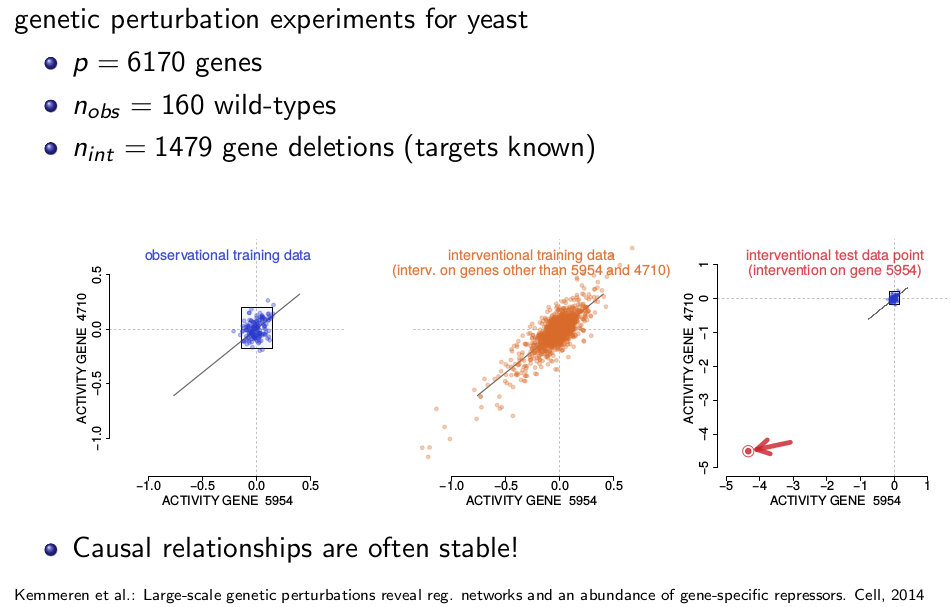
上面这个研究中，有6170个基因，图中的横坐标表示基因5954的活性，纵坐标表示基因4710的活性。有160笔观察数据，左边这张图就是观察数据画出来的，可以发现，两个基因的活性表现出了一定的相关性。这个实验还有1479笔干预数据，即对一些基因做删除动作，总共有1479个不同的删除动作，中间的图则是被干预后基因5954和4710的活性的变化，更可以发现这两种基因的活性是强相关的。
这个研究的目的其实是要发现这些基因之间的因果关系。但非常有意思的是，这些数据可以支持一个论点，即因果关系通常在系统中是稳定的。在试验中，基因5954是基因4710的因，右图中当对基因5954做了干预后，4710的活性也随着产生了明显的变化。由中间那幅图的实验，1479次的干预来看，不论删掉系统中哪个部分，基因5954和基因4710都是强相关的。可见因果关系在系统中是一种稳定的关系。
举个例子，有如下因果关系：x<-w->z->y，z和y是因果关系，x和z之间不存在因果关系，则改变x的状态，对z和y的状态不会造成影响，改变w的值，那么z和y会跟着一起改变。
此系列未完待续，敬请关注^_^。
声明：所有图片均来自Jonas Peters的课件，没有原创图片和公式。
参考：
[1] Jonas Peters, University of Copenhagen, Mini course on Causality, Laboratory for Information & Decision Systems (LIDS) and Models, Inference & Algorithms of the Broad Institute, MIT, 2017
[2] Judea Pearl and Dana Mackenzie, The Book of Why, 2018
Comments