一、分布和因果图
例1. 海拔和温度
假设，海拔和温度的分布及因果关系是已知的，且如下图所示：
海拔和温度存在因果关系，平均每上升100米，温度下降0.6摄氏度。上图中左图是海拔和温度的分布情况，右边是因果图。Nx，Ny为独立同分布，假设它们都服从期望值为0，标准差为1的标准正太分布。X，Y服从二维正太分布如上图所示。
如何对这个系统进行干预呢？直接确定X的值即可。
当确定了X的值后，Y的分布也会产生变化，Y服从均为为-16，标准差为1的正太分布。
也可以对Y进行干预，使Y服从均值为2，标准差为2的正太分布：
那么X和Y之间的因果关系就被破坏了，因为要改变Y的分布，比如你装了一台超级大的空调，使得Y服从了这样的分布，那么海拔的变化便不再有影响力。海拔和温度之间的因果关系就不存在了。海拔和温度就变成了两个独立的变量，X，Y的联合分布也变成了上图所示。
可观察到的所有变量X1，…，Xd的分布式集，我们称之为P，即下图左边的所有公式。
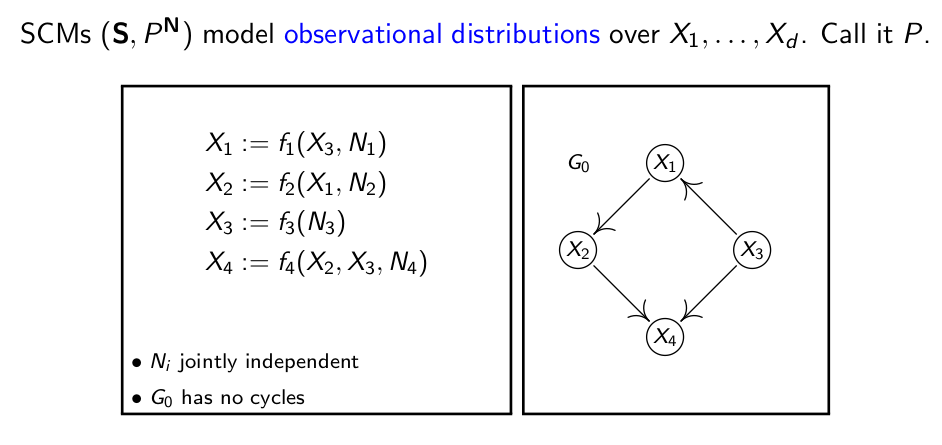
当我们要对系统进行干预时，即改变某些变量的值或者和其他变量的关系，如把X1的值固定在0上，分布式集则变为Pdo(X1:=0)，变量之间的因果关系也会产生相应的变化。
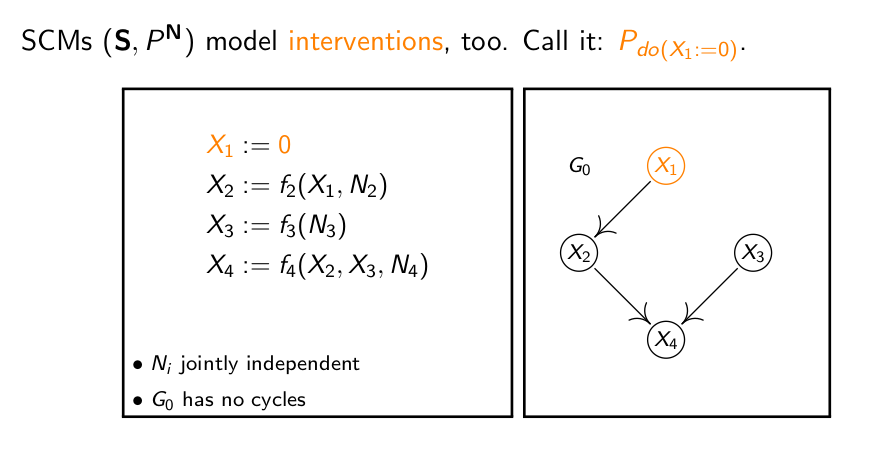
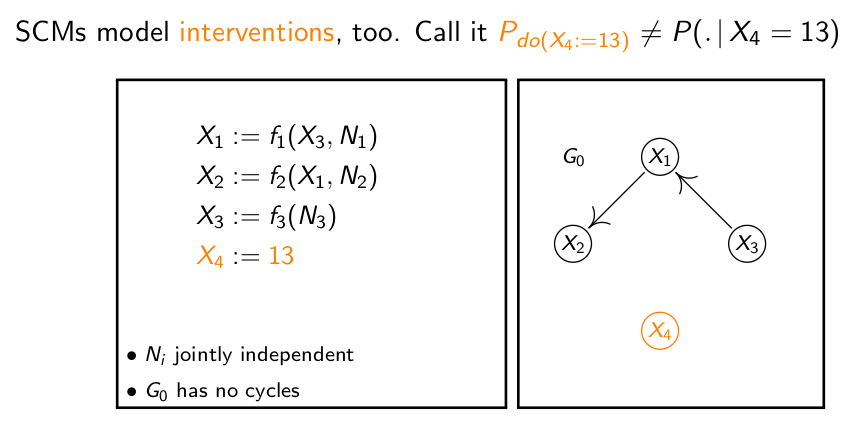
Pdo的下标do表示的是干预的这个动作。下图中将X4这个变量的值通过干预使之固定为13。为什么要加一个do的下标来表示干预呢，因为直接写成P(X4:=13)，很容易被误理解为P(.|X4=13)，即X4=13时系统的状况。Pdo(X4:=13)与P(.|X4=13)完全是两码事。
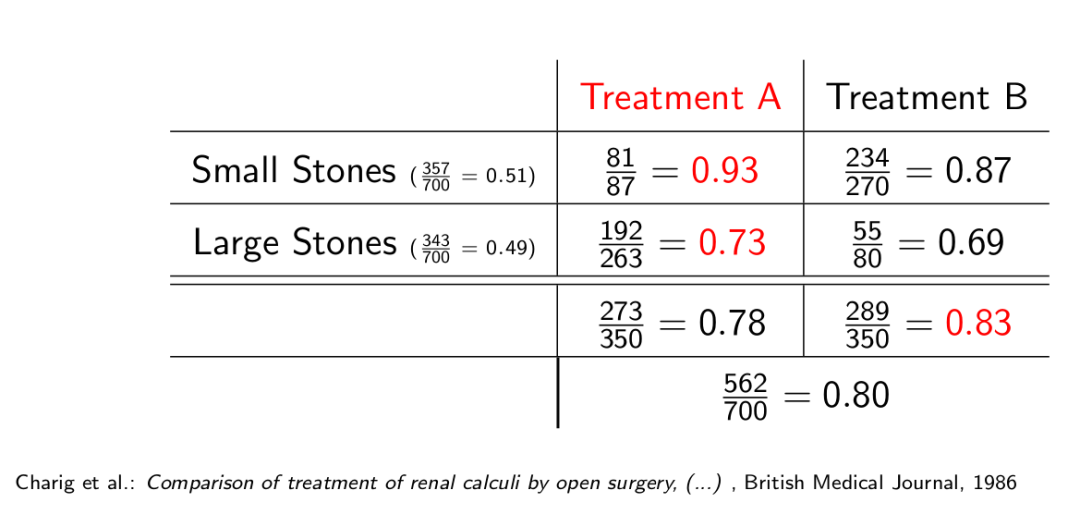
例2. 肾结石
关于这个例子，上一节MIT因果迷你课笔记 —— 相关和因果中有做一些讨论。
假设我们现在只知道肾结石治疗的因果图，不知道每个变量的分布情况。肾结石治愈率受治疗方案和结石大小影响，而结石大小又对治疗方案的选择有直接的影响。
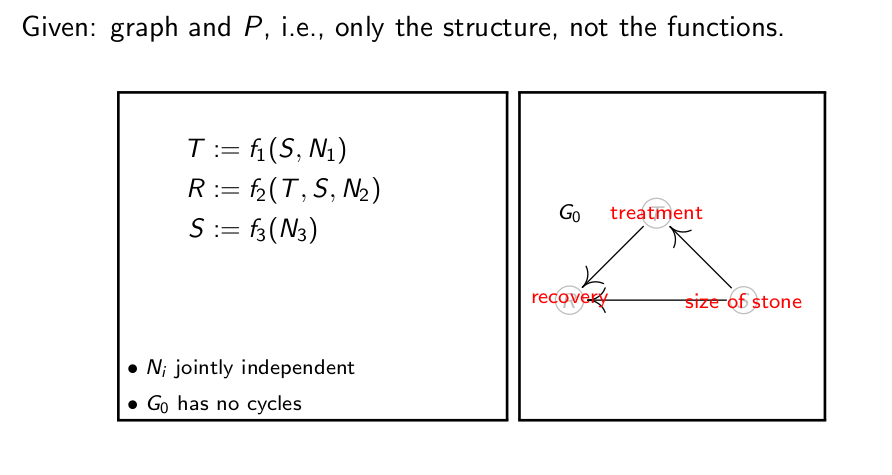
我们想知道的是，治疗方案A和治疗方案B的治愈率分别是多少，那么它们在这个场景中则不能简单地用P( R =1 | T =A )和P( R =1 | T =B)去表示治疗方案A和B的治愈率。而应该用Pdo(T:=A)(R=1)和Pdo(T:=B)(R=1)来表示，因为我们想知道的是，如果我们不管结石大或小，选择治疗方案A或B能获得的治愈率，如下图：
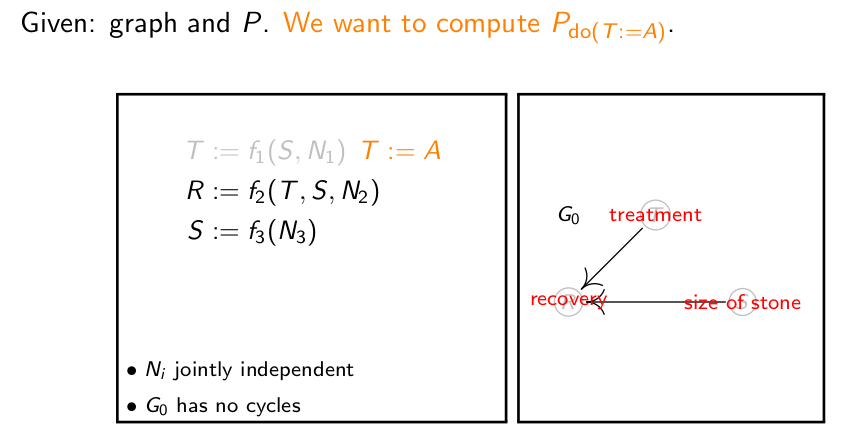
现有一些样本统计结果：
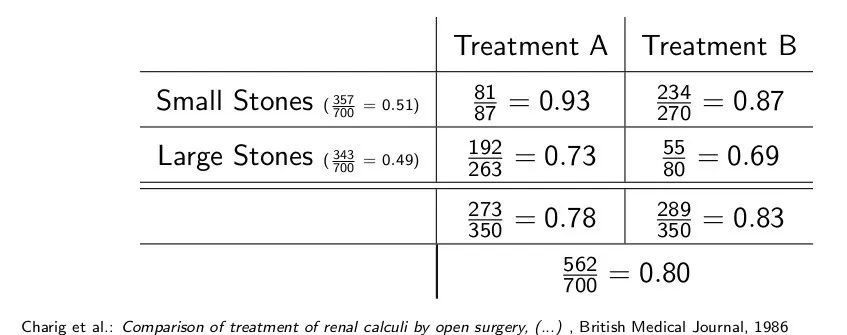
Pdo(T:=A)(R=1)的值的计算如下：
说几个比较重要的点，Pdo(T:=A)(S = s, T = A) = Pdo(T:=A)(S = s)，是因为有了do(T:=A)这个干预后，S和T相互独立。Pdo(T:=A)(S = s) = P(S = s)，因在因果关系中S不受治疗方案和治愈率的影响。Pdo(T:=A)(R=1|S = s, T = A) = P(R=1|S = s, T = A)的道理也是一样，这样的干预并没有改变R和S还有T之间的因果关系。最后得到的Pdo(T:=A)(R=1)不等于P(R=1|T=A)，因此，当我们想进行主动干预的时候，比如主动选择治疗方案的时候，因果推理就十分有必要了。
将上面的现象一般化，即可得到下面有效调整集(valid adjustment set)的定义，对于上一例，结石大小就属于(T，R)的有效调整集。
为什么需要定义一个有效调整集？在探索X，Y之间的因果关系时，需要计算Pdo(X:=x)(y)，而去场景中干预X做实验，有时候是不现实的。比如，假设一个人去了医院发现了肾结石，但医院检查结石大小的机器恰好坏了，他得在A，B方案中选择一个，因此他得知道A，B方案的治愈率，那个时候再去干预X做实验来获得X和Y之间的因果关系显然是不现实的，他拥有的只有过往的一些统计数据，还有统计变量之间的因果关系。那么是哪些变量使得这些统计数据不能直接用来表示X和Y的因果关系？如何去掉这些变量造成的影响，通过对已有数据的计算来得到X对Y的影响？
符合上述条件的即为有效调整集，那么怎么样快速有效的找到有效调整集，下面给出了一个方法，但注意这个方法不能找出所有的有效调整集。
结合下面这张因果结构图理解一下有效调整集的概念。
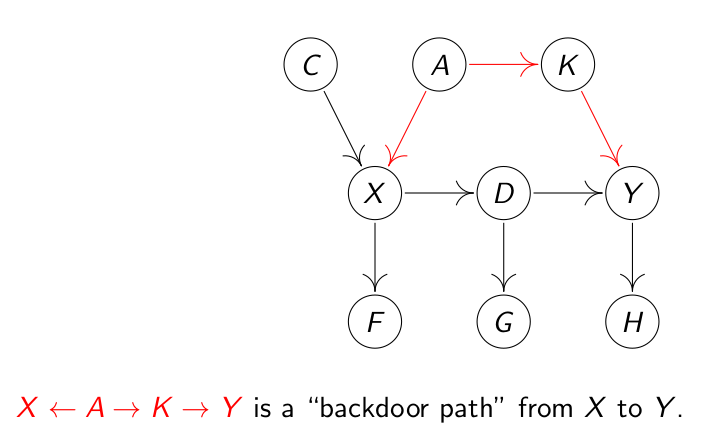
X<-A->K->Y被定义为“backdoor path”，上面因果图中，人们其实并不关心其他的因果关系，他们只关心X和Y的因果关系，就像肾结石那例，我们并不关心医生依照结石大小会对方案做出的选择，我们只想知道每种治疗方案的治愈率。因此我们想知道的是X->D->Y这条关系，X对Y有什么样的影响。对于A对X造成的影响，我们不关心，因此，X<-A->K->Y这种同时影响着X和Y的因果关系链被称之为“backdoor path”。
上图因果关系中的有效调整集都有哪些呢？这里举三个有效调整集，{A，C}，{K}，{F，C，K}，这三个并不是全部的有效调整集。{A，C}这组有效调整集即X的父结点的集合，为什么取X的不包含Y的父节点的集合能得到有效调整集呢？因为有效调整集必须能够切断所有的“backdoor path”。在这一例中，能够切断“backdoor path”的结点是A和K，而其他结点都是可有可无的，比如C或F在不在有效调整集中，都不会影响调整集的有效性。
那么为什么要切断所有“backdoor path”呢？当我们对X进行干预的时候，A对X的影响就被切断了，A只对Y产生影响。do(X:=x)这个动作改变了因果关系，舍掉了A对X能产生的影响，所以计算中也应该排除A对X产生的影响。值得注意的是，虽然A才是关键的影响着X的结点，但是统计计算的时候受A影响又影响着Y的K也可以作为有效调整集的必要点，因为它的状况可以反馈A的状况，如果A不易被观察到，观察K也可以得到正确结果。
另外，D，G，H都不应该出现在有效调整集当中。D，G会直接或者间接地切断X和Y的关联，H则会暴露Y。
例3. 烟草和肺癌
再回到烟草和肺癌这个经典案例：
关于这个例子，上一节MIT因果迷你课笔记 —— 相关和因果中有做一些讨论，在1950年的时候有这样一篇文章发表，详细分析了吸烟和肝癌之间的相关性，现在我们知道，相关不一定构成因果，可能是由潜在的原因同时导致了吸烟和肝癌。
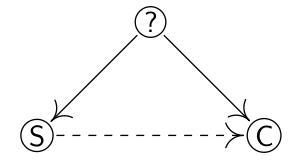
而这篇文章的优秀之处在于，结合了各种可能的潜在原因，比如将各种压力，性别，地域等因素列为观察的变量。即增加不同的调整集，发现吸烟和肝癌总是强相关，即，找不到有效调整集可以改变吸烟和肝癌之间的相关性。既然吸烟有害身体健康，那么政府就想让烟草公司纳税，烟草公司为了避税，把这个潜在原因归到了基因上，即某种基因导致了一个人既喜欢吸烟，又容易患肝癌，我们今天来看当然是非常荒诞的，但是当时科技还不怎么发达，人们对基因的认知也很有限，就这样被烟草公司忽悠了。这里Jonas Peters推荐了一本书《Merchants of Doubt》，不能尽信科学家，他们也会被利益驱动去做一些违背道德的事情，商人和政客就更不用说了。
例4. 坏血病和柠檬
在1747年的五月，James Lind在一艘行驶在海上的船上，对患有坏血病的12名船员做了一个随机化实验，将十二名船员随机分成六组，配给不同的食物，得到的结果是，每天获得柠檬的病人，病情明显好转。他可能意识到调整饮食可以治愈这种病，但是又不知道如何调整，才能治愈这种病。因此他设计了一个随机化实验，这种实验方式后来被广泛应用于医疗领域。
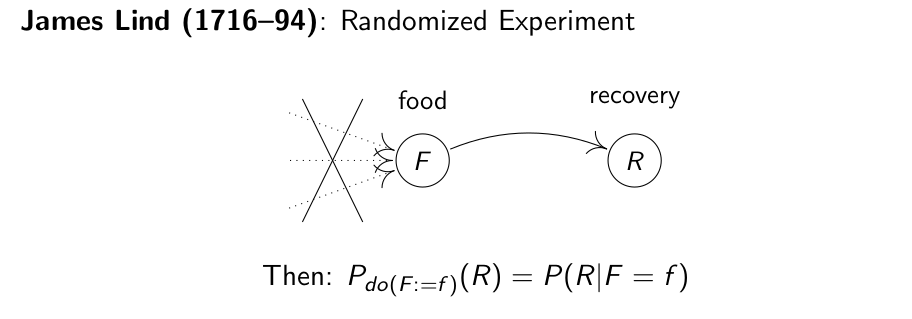
随机化实验的价值在于，因果关系是复杂的，但如果你把船员随机分组，然后再配给食物，那么食物配给就不受任何因素影响了，即切断了因果图中所有到food这个结点的父结点，那么观察到的food和recovery之间的因果关系就不需要有效调整集来调整了，得到的相关性就是它们之间的因果关系。
接下来是一些小概念，如果这两个模型有相同的概率{概率和干预}分布，我们称两个模型概率上{干预上}对等。在干预时，随机化干预能得到正确的因果关系。
下面用四种方式定义了认定X是Y的因需要符合的条件。(i)中X和Y中间的符号是dependence的意思，去掉斜杠是independence。
思考：如果X和Y之间存在因果关系，那么X和Y之间因果关系的强度又该怎么定义和计算？
也许是：
<div align=center>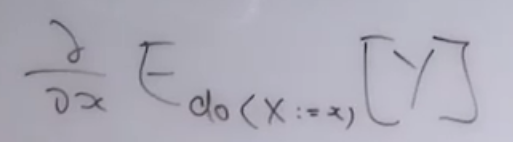
</div>
工具变量(Instrumental Variables)
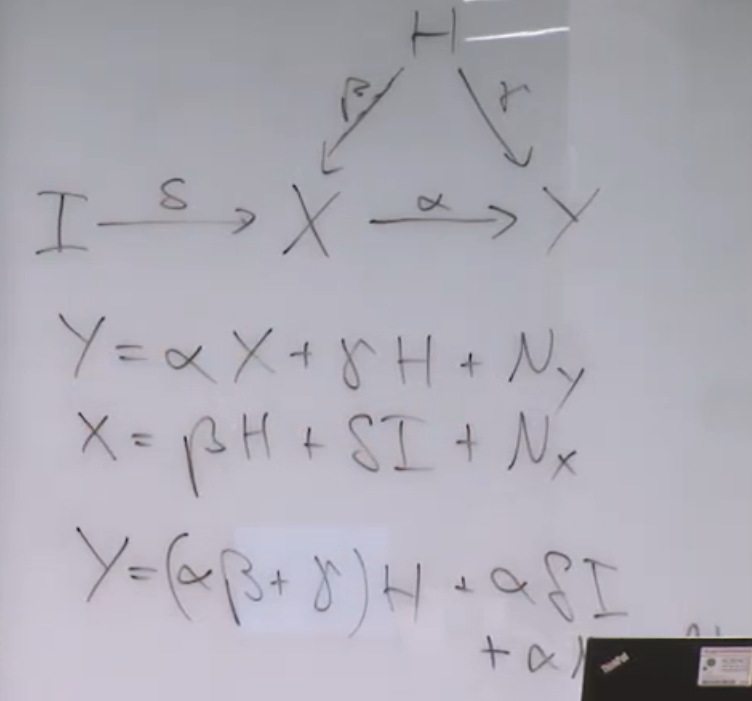
我们依然是想计算X，Y之间的因果关系，以及它们之间的系数，但是由于H不好观察，X不好控制，我们没有办法通过控制X来得到它和Y之间的关系，这个时候如果有个变量I，它独立于X，H，Y这个系统，那么就可以通过控制它得到X和Y之间的关系。这种变量被称之为工具变量。
反事实(Counterfactuals)
《生活大爆炸》第四季里有一段关于反事实的游，感兴趣的搜索着看一下。
关于反事实，上一节有提过，这个概念对照的是人类反思和想象的能力，这个能力非常重要，是让我们有洞察力的关键，不过也有很多副作用。
对应到SCM，可以做如下定义：
通俗地说，反事实就是对SCM中分布公式中的随机部分做定义，从而改变因果关系。举个例子：
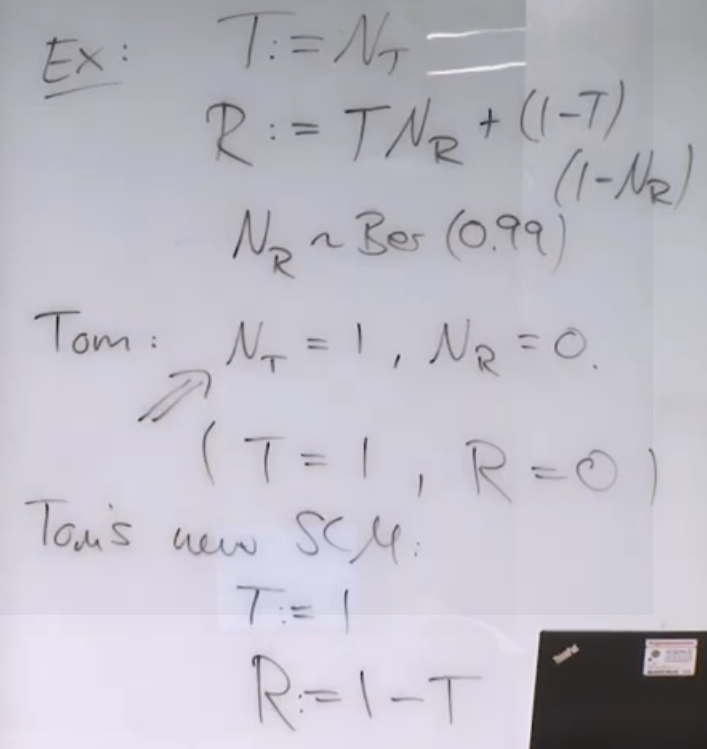
如上图，假设一种病，是否治疗服从NT随机分布，如果治疗，治愈率为99%，如果不治疗，治愈率为1%。如今，Tom也得了这种病，而他恰好就是一个特例，如果他治疗，治愈率是0，如果他不治疗，反而会好。但这只有发生后才明确知道，因此，在Tom接受治疗，死亡后，我们说如果Tom不治疗，那么他反而会痊愈，这就是反事实。
接下来总结一下这个部分：
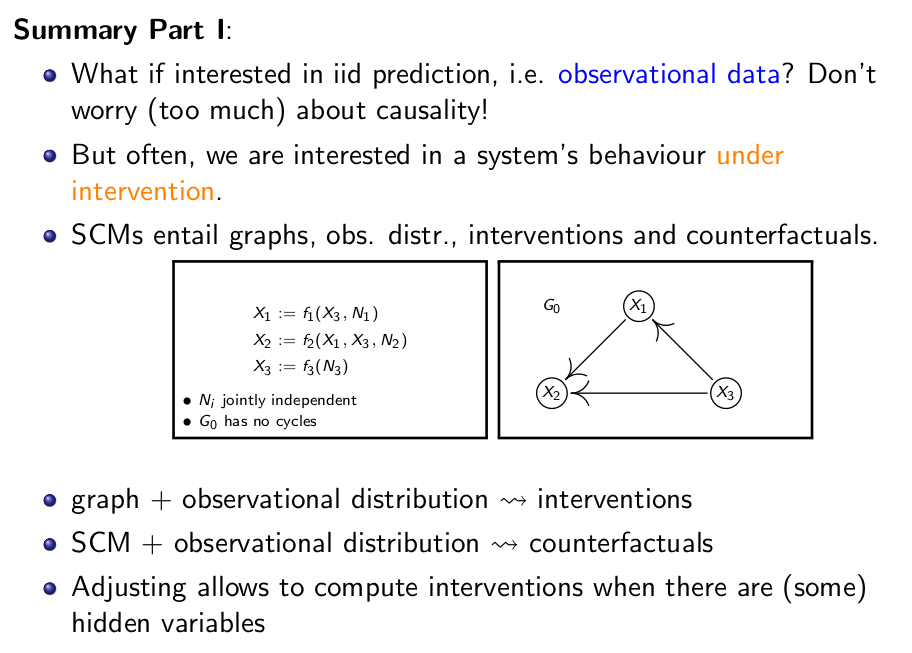
1. 因果关系不是什么时候都有必要研究，很多时候我们只需要知道相关性，比如你想让机器人把猫认出来，相关性即可，你想要机器人把猫画出来，可能会需要因果关系。因果关系通常是，我们想对环境进行干预，并想知道干预后的结果，才有必要去了解的。 2. 当我们有了因果图和变量的分布公式后，我们就能推演出干预后变量分布的变化。反事实也是如此。
下面这个研究很有趣，想知道死神走多快吗？可能是0.82m/s，要走的比他快哦，被赶上就完蛋了。
此篇上一节为：MIT因果迷你课笔记 —— 相关和因果
此系列未完待续，敬请关注^_^。
声明：所有图片均来自Jonas Peters的课件，没有原创图片和公式。
参考：
[1] Jonas Peters, University of Copenhagen, Mini course on Causality, Laboratory for Information & Decision Systems (LIDS) and Models, Inference & Algorithms of the Broad Institute, MIT, 2017
[2] Judea Pearl and Dana Mackenzie, The Book of Why, 2018
[3] 我是啤酒，MIT因果迷你课笔记 —— 相关和因果，2020
Comments