系列首篇:MIT因果迷你课笔记 —— 相关和因果
上篇:MIT因果迷你课笔记 — 因果归纳和机器学习之半监督学习
这是这门课最后一部分的内容,因果归纳和机器学习。
总共分四个部分,这是第二部分,讲因果归纳和half-sibling regression。
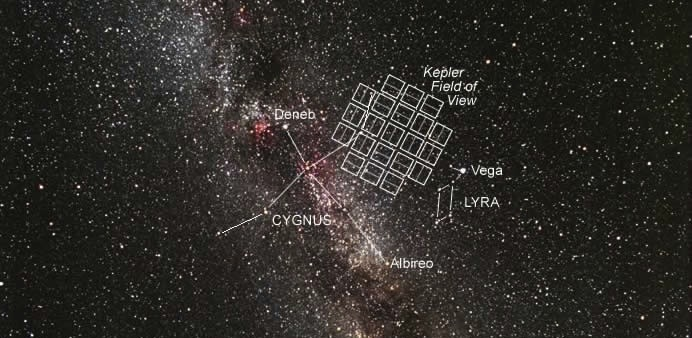
先考虑一个关于系外行星的研究。我们有一个开普勒望远镜,以某个角度在观察宇宙,任务是发现系外行星。
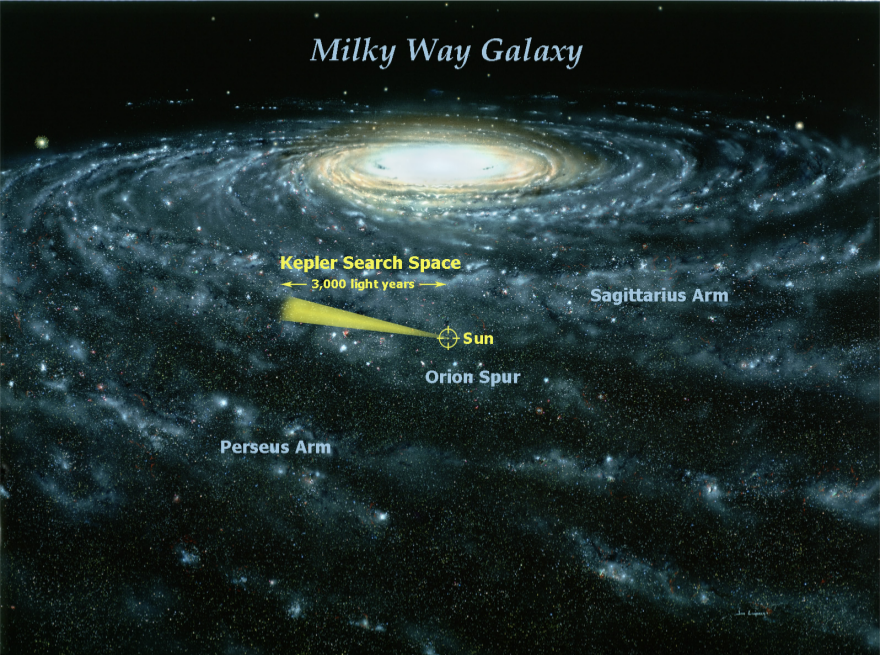
该望远镜的观察范围是3000光年。
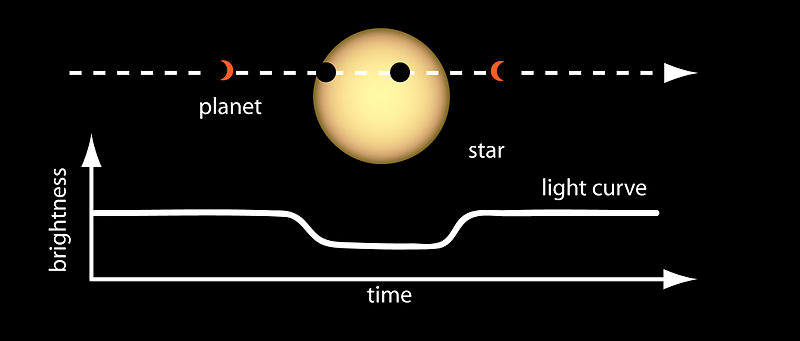
那么理想状况下,如何判断一个恒星周围有行星在绕行呢?观察这个恒星的光的强度,如果如上图所示,间隔固定时间就有一段时间光的强度降低了一些,那么可以认为,有一个行星在绕这个恒星运行。
但是,理想归理想,现实很骨感,现实中观察到的数据充满了噪声,无法用上面那种简单的逻辑来分辨出行星的踪迹。
接下来,我们分析一下这个案例的信息构成。
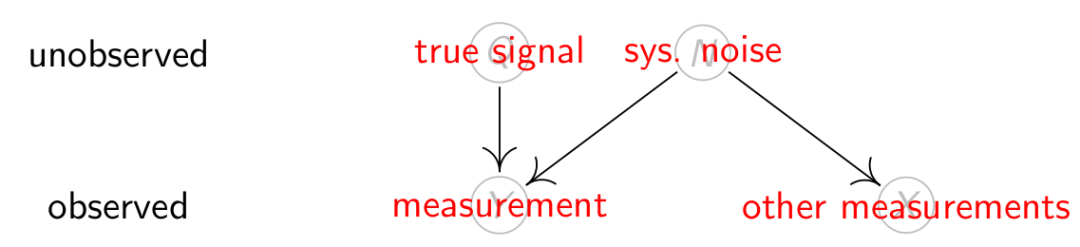
我们没有观察到的信息,由我们需要的恒星系统的光强及系统噪声组成。我们观察到的信息,由对该恒星系统的观察和对宇宙其他部分的观察组成。对该恒星系统的观察由该恒星系统的光强和系统噪声组成,其他观察由系统噪声组成。
这些信息又呈什么关系呢,因为系统噪音和true signal是来自不同星体的信息,且间隔很远,相互之间的影响可以忽略不计,因此true signal和系统噪音是相互独立的。因此观察到的信息中measurement和other measurements中的共同部分一定是系统噪音。
将上图公式化,得下图:

我们要求的是Q,怎么得到呢?移除Y中所有可以被X解释的部分。


上图中展示了三种方法,第一种就是找到X和f(N)之间的映射关系,计算出f(N),解出Q,这无疑是最理想的一种方式。第二种,假设X中只有少量噪声。第三种,假设有多个观察,即多个X。
具体去噪方法可以参考最后一幅图中的参考文献,这里就不仔细展开了,之后的几幅图展示了一下实验效果:
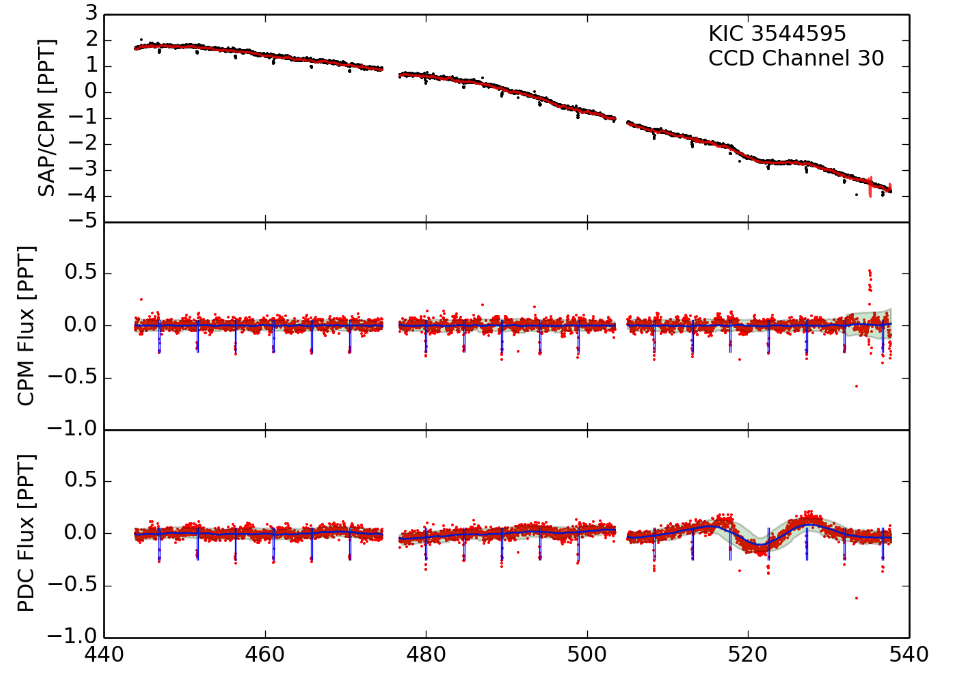
横轴是时间,中间断裂的部分是仪器的观测机制造成的,纵轴是观测数据,第一幅图是原始数据,第二幅图是去噪后的结果,可以发现,是可以明确发现行星的踪迹的。下图也一样:
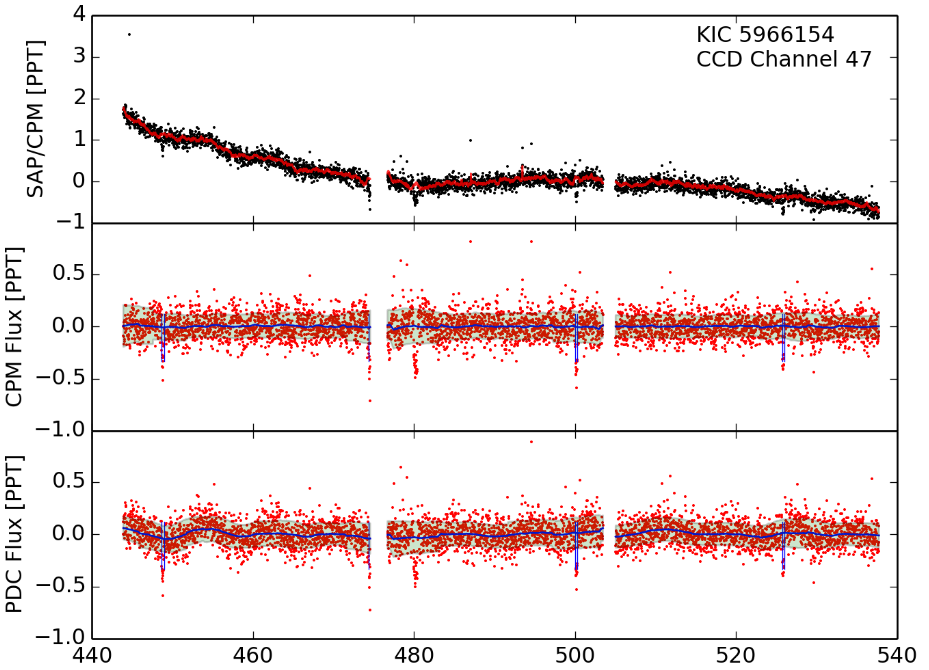
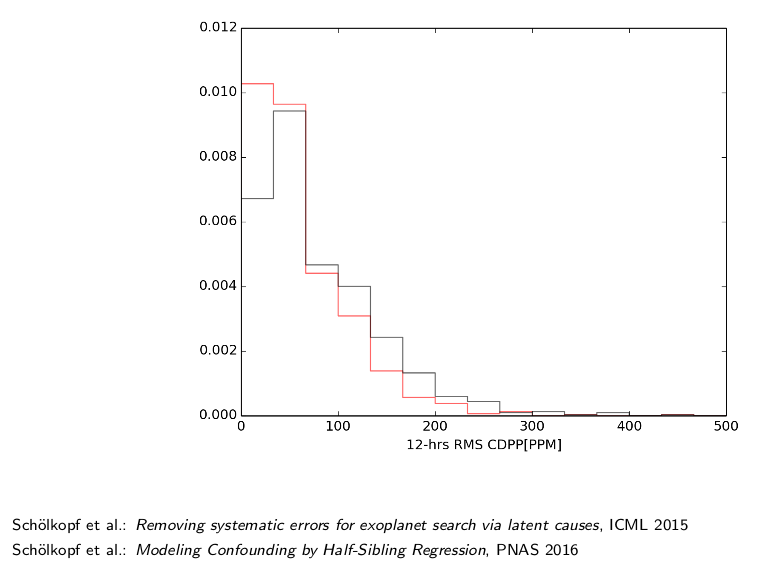
上面这幅图就不做具体解释了,感兴趣可以看图中参考文献。
系列首篇:MIT因果迷你课笔记 —— 相关和因果
上篇:MIT因果迷你课笔记 — 因果归纳和机器学习之半监督学习
记:公式上上下下有不匹配的地方,因为截自不同的参考文献,所以写法会有出入,打公式太累了,我放过了自己。
声明:所有图片均来自参考,没有原创图片,公式和定理。
参考:
[1] Jonas Peters, University of Copenhagen, Mini-course on Causality, Laboratory for Information & Decision Systems (LIDS) and Models, Inference & Algorithms of the Broad Institute, MIT, 2017



Comments