系列首篇:MIT因果迷你课笔记 —— 相关和因果
上篇:MIT因果迷你课笔记 — 因果归纳和机器学习之half-sibling regression
这是这门课最后一部分的内容,因果归纳和机器学习。
总共分四个部分,这是第三部分,讲因果归纳和强化学习。
这部分有三个案例:
一:肾结石案例
这个案例之前提到过,先回顾一下:
肾结石的两个治疗方案:
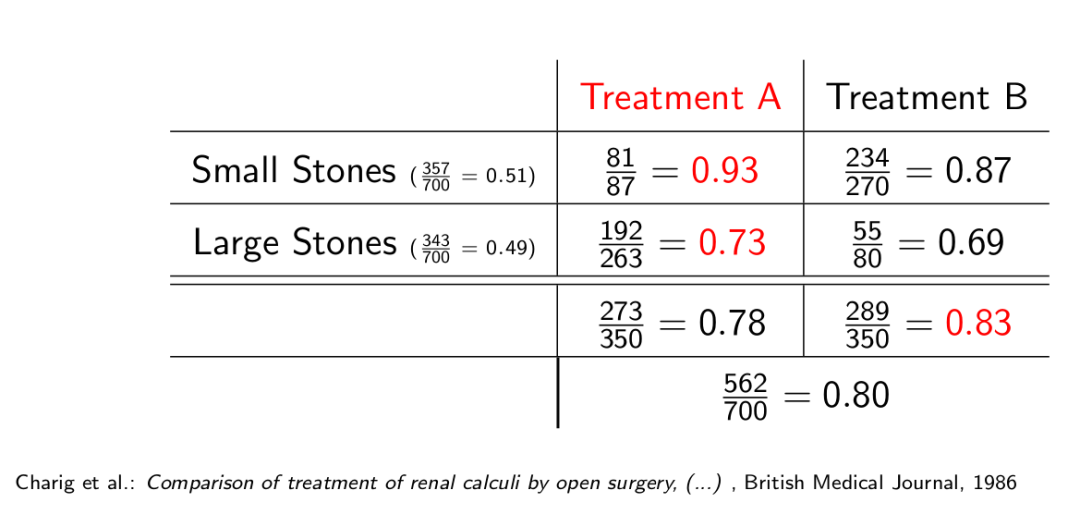
肾结石有两个治疗方案,A和B,如果看总的治愈率会发现,B方案明显好于A方案。但是肾结石的石头又可分为大小两种情况,从这两种情况的治愈率来看,A方案又明显好于B方案,造成这种结果的原因是,治愈率不但和治疗方案有关,还和结石大小有关,A方案的治愈率虽然高,但主要用在了治愈率较低的大结石,而B方案则主要用在了治愈率较高的小结石,因此,简单地比较总的治愈率,对A方案来说是不公平的。治愈率,结石大小,和治疗方案的因果关系可以用下图表示:
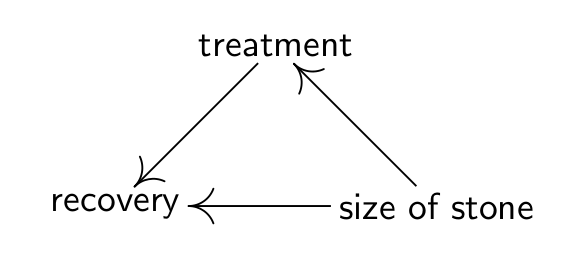
公式化上图,得:
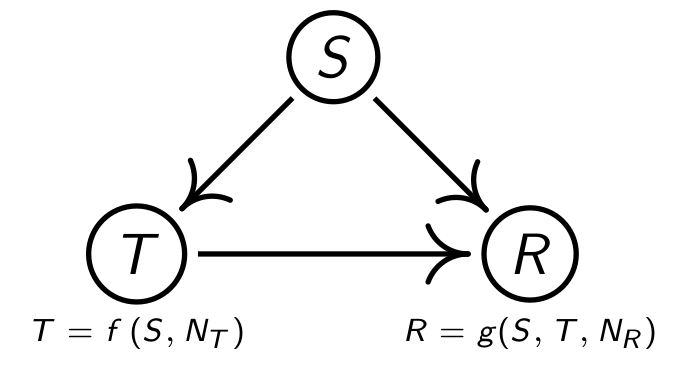
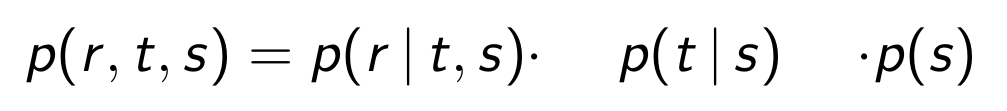
P(r,t,s)可以按上面公式展开,其中p(r|t,s) = R = g(S,T,NR),p(t|s) = T = f(S,NT),现在想对治疗方式进行干预,那分布该如何变化:
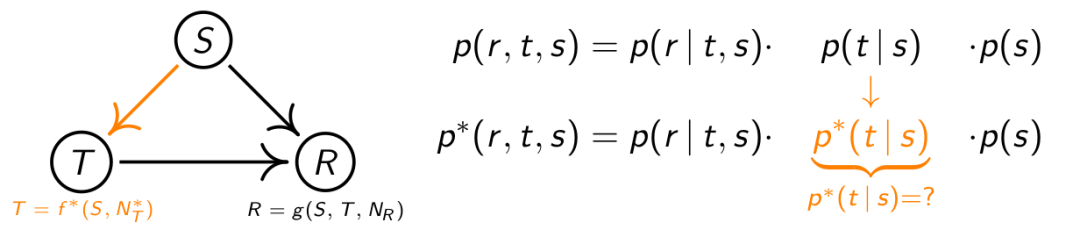
也就是说,如果想干预治疗方式,那么改变的是治疗方式的分布函数,如果想干预治愈,那么改变的是治愈的分布函数。可以用这种方式去求解治疗方式的最佳选择。
二:Blackjack
这是一个扑克牌游戏,又名21点,源于法国,现已流传到世界各地。规则如下:

该游戏由 2 到 6 个人玩,使用除大小王之外的 52 张牌,游戏者的目标(Goal)是使手中的牌的点数之和不超过 21 且尽量大。
每张牌都有点数, 2 到 10 的牌的点数就是其牌面的数字;J 、 Q 、 K 的点数是 10;A 有两种算法, 1 或者 11 ,如果 A 算为 11 时总和大于 21 ,则 A 算为 1 。例如 ( A, 8 ) 是 19 点,( A, 7, J ) 则为 18 点。
首次发牌(Dealing)每人2张牌。庄家以顺时钟方向向众玩家家派发一张暗牌(即不被揭开的牌),然后向自己派发一张暗牌,接着庄家会以顺时钟方向向众玩家派发一张明牌(即被揭开的牌),之后又向自己派发一张明牌. 当众人手上各拥一张暗牌和一张明牌,庄家就以顺时钟方向逐位向玩家询问是否再要牌(Hit)(以明牌方式派发)。在要牌的过程中,如果玩家所有的牌加起来超过21点,玩家就输了(俗称爆煲Bust),游戏也就结束了。该玩家的注码归庄家。
如果玩家无爆煲,庄家询问完所有玩家后,就必须揭开自己手上的暗牌。若庄家总点数少于17点,就必须继续要牌;如果庄家爆煲,便向没有爆煲的玩家,赔出该玩家所投注的同等的注码。如果庄家无爆煲且大于等于17点,那么庄家与玩家比较点数决胜负,大的赢(例牌除外)。一样点数为平手,各自取回赌注。
停牌(STAND):不再拿牌。在任何情况下,玩家可选择停止要牌。
分牌(SPLIT):玩家再下一注与原赌注相等的赌金,并将前两张牌分为两副单独的牌。这两张牌的点数必须相同(即一对8、一对K 或一对Q,某些玩法中两张10点的牌如一张10一张Q时也可分牌)。但分牌后的黑杰克,只能作普通21点计算,其赔率只是1 赔1 。
双倍下注(DOUBLE或DOUBLE DOWN):玩家在拿到前两张牌之后,可以再下一注与原赌注相等的赌金(如果觉得少可以加倍),然后只能再拿一张牌。如果拿到黑杰克,则不许双倍下注。(部分玩法中拿到3张或3张以上也可选择双倍下注,但同样只能再拿一张牌)
**例牌(BlackJack**):如果玩家手中的一张暗牌和一张明牌分别是一张A牌(可作11点)和一张十点牌(K、Q、J、10),这副牌叫做二十一点,例牌(BlackJack)。该玩家可向庄家报到,庄家须向该玩家赔上1倍(有些,1.5倍)注码。
举例:

图中最左边的玩家有两手,庄家点数是17,这个玩家的两手分别是16和21,毫无疑问21这手赢了庄家,中间超过21点,爆煲,输了,(J,K)加起来20,赢了,最右边16,平了。
那么,如何取得这个游戏的最佳策略呢?

首先,采用随机策略,进行一些游戏,取得一些样本数据p = p(X,Y,Z)。X:当前的状态,比如玩家手里的牌或所有玩家手里的牌,桌面上出现过的牌,庄家总共用了几副牌等等,Y:对当前状况采取的策略。l = l(X,Y,Z)是收益方程,p策略,即知道了现在的状况后,为了争取最大收益或最小损失,选择的策略,如拿牌,停牌,分牌等,p则是用样本优化后我们求的策略。Epl表示在这种策略下的期望收益或损失。
期望收益的计算可以如下:
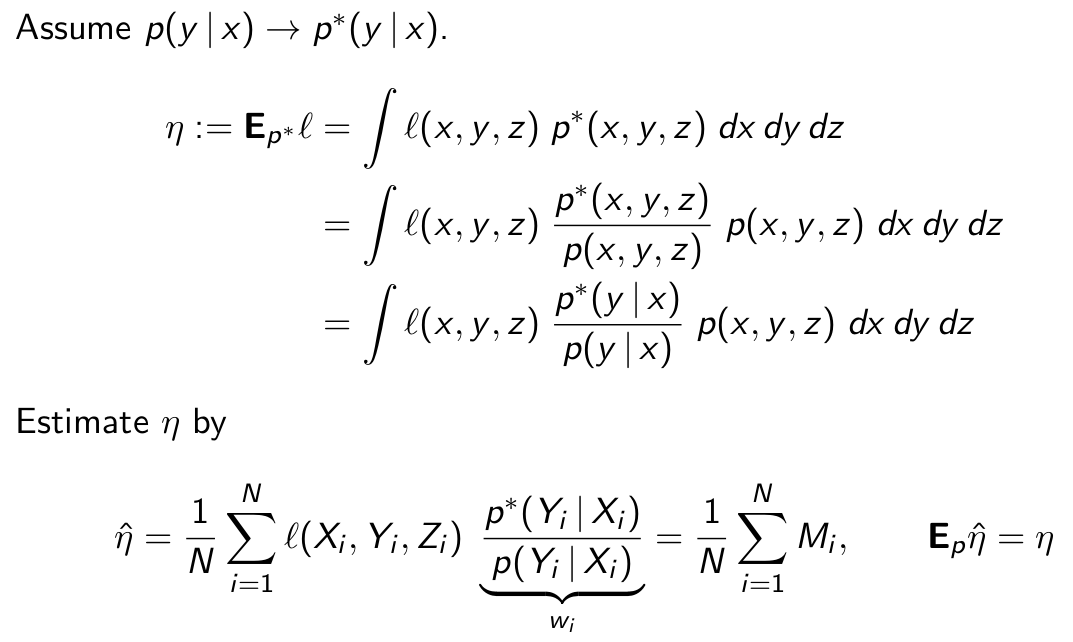
这里的每一步推导就不展开说了,我们想得到的是p(y|x),已知的是p(y|x),我们希望用p(y|x)替换p(y|x)后,Ep*l的值能变大。

训练是一个循环往复的过程,刚开始的策略是随机策略,然后进行一些游戏后,用已有的样本进行策略优化,将优化的策略替换原本的策略,再进行一些游戏,进行这些游戏的时候,一部分策略用的是之前优化后的策略,但依然会保留随机性,即有一部分决策是随机的选择。再用新得的样本优化现用的策略,将优化后的策略替换原本的策略,如此反复,直到期望收益不再会因为这个过程提高。
这个游戏的因果结构如下(简单的):
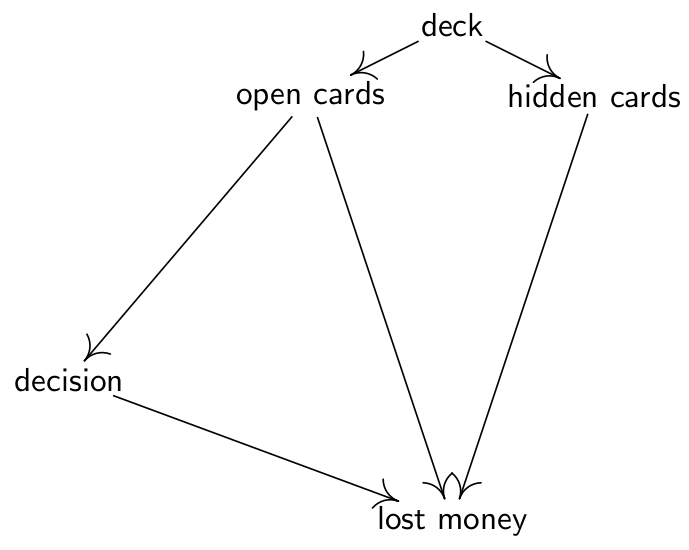
最后的输赢取决于你的策略,桌面上的明牌和暗牌。也可以在因果图中补充一些信息,比如,就这个游戏而言,输赢和牌的花色没有关系。
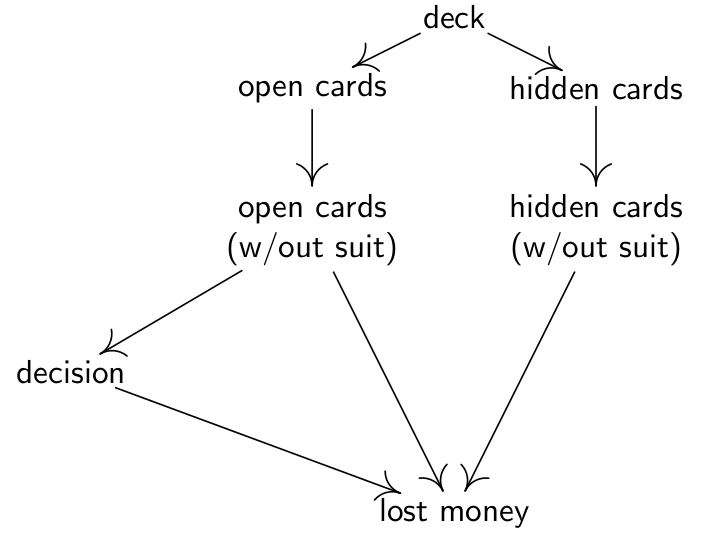
下图是增强算法在优化这个游戏策略上的表现:
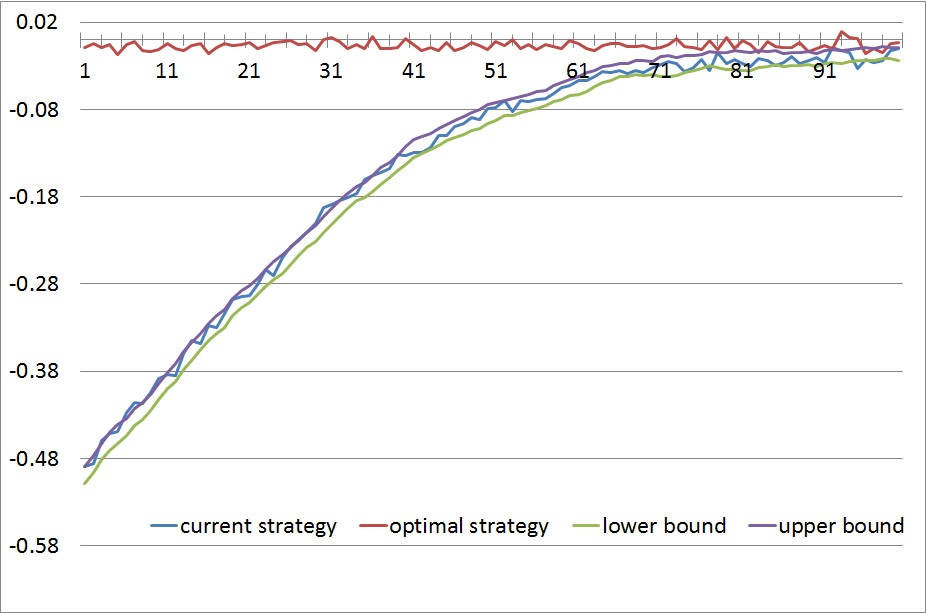
接下来看最后一个例子:
三:广告推荐
当我们使用搜索引擎搜索一些东西的时候,或者做一些其他和网络互动的事情时,经常会被推送一些广告,如下图:
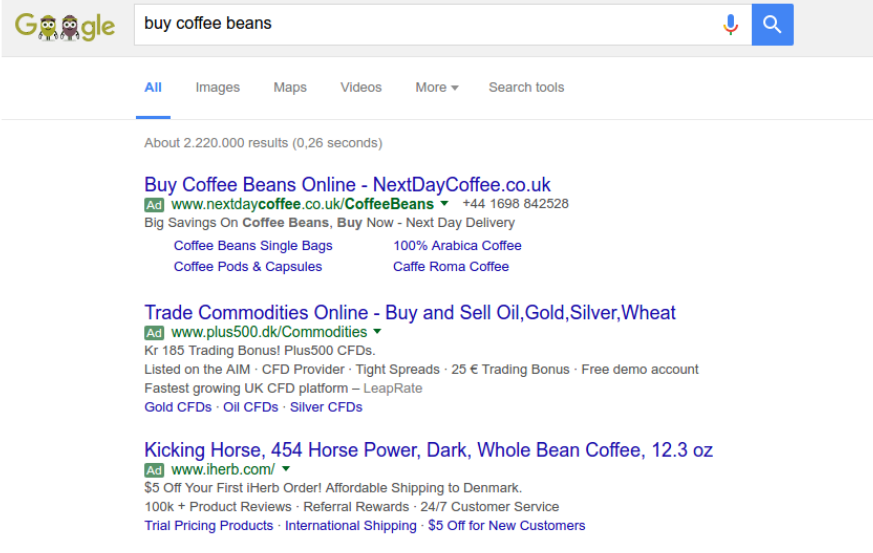
可以通过研究推送广告过程中的因果关系来优化模型:
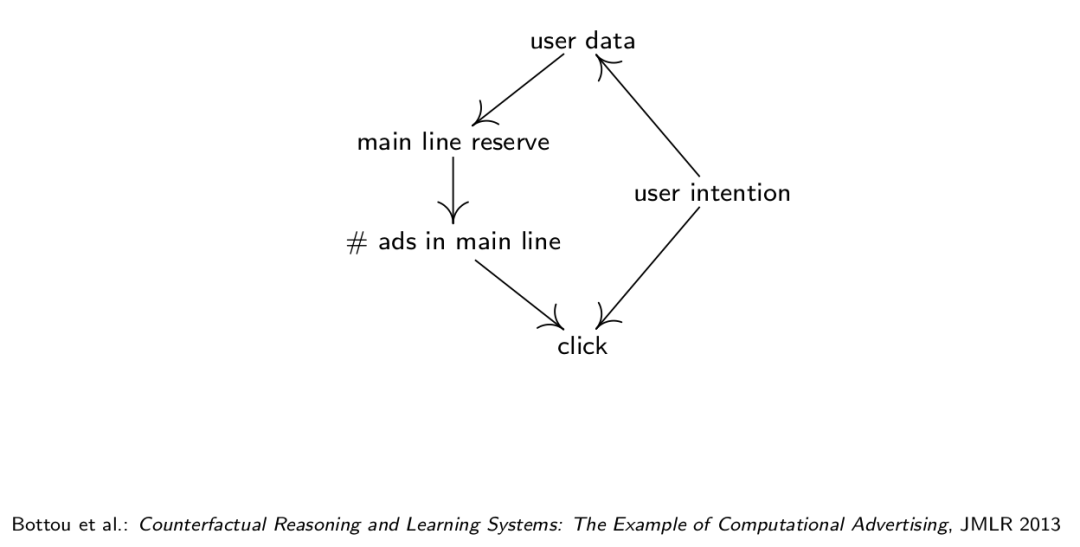
用户的意图会决定用户的操作,并产生一些数据,而通过分析用户的数据,我们来决定给他推送什么样的广告,以及推送多少广告,而这些推送又会一定程度上决定用户的行为。
user intention指用户意图,user data指和用户相关的数据,main line reserve指保留多少及什么样的空间给广告,#ads in main line推荐的广告数量,click是用户的点击。这只是一个简单的广告推荐的因果图,广告推荐的因果图可以更复杂,比如加上广告的内容,类别等等。这样的推荐系统,也可以用强化学习的方式来做,保留一点随机性,可以发现更多的可能。我们最终想要的是更多的点击,而不是把广告推送出去。
下面对广告系统做了一点简单的实验:
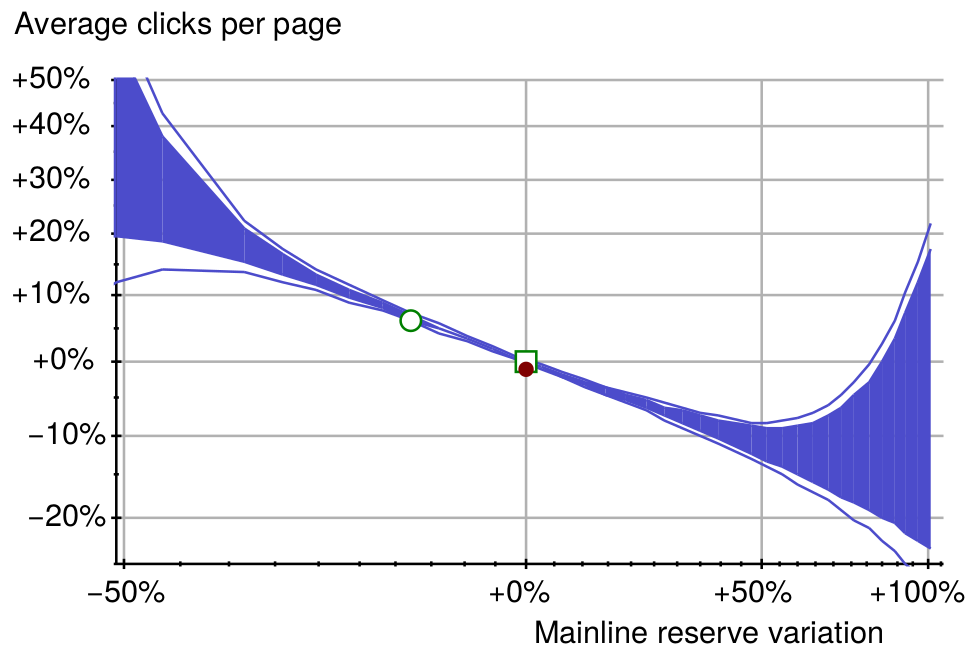
(0,0)位置表征的是这个广告系统的初始状态,增加或减少广告区域,可以发现,减少广告区域可以增加广告的点击量。蓝色区域表示的是区间,因测试数据并不充分,因此只能表达出调整广告区域后点击量所在的区间。
由因果图可以发现,广告区域决定了广告的数量,而广告数量才是决定点击量的直接因素。那么如果直接用广告数量来进行实验,实验结果如何:
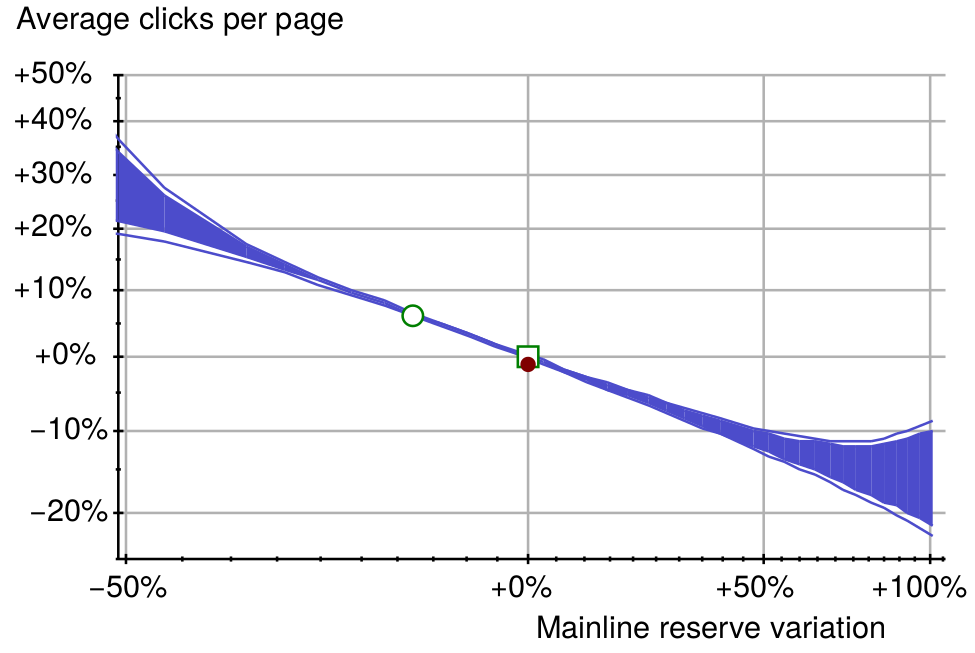
趋势还是那个趋势,区间大大缩小了。因此,准确地使用因果关系来分析问题,效果可能会更好。
系列首篇:MIT因果迷你课笔记 —— 相关和因果
上篇:MIT因果迷你课笔记 — 因果归纳和机器学习之half-sibling regression
记:公式上上下下有不匹配的地方,因为截自不同的参考文献,所以写法会有出入,打公式太累了,我放过了自己。
声明:所有图片均来自参考,没有原创图片,公式和定理。
参考:
[1] Jonas Peters, University of Copenhagen, Mini-course on Causality, Laboratory for Information & Decision Systems (LIDS) and Models, Inference & Algorithms of the Broad Institute, MIT, 2017
[2] cplwsy, 21点Blackjack玩法,百度经验,2017




Comments