系列首篇:MIT因果迷你课笔记 —— 相关和因果
上篇:MIT因果迷你课笔记 —— 基于不变性的因果预测(invariant causal prediction)
这是这门课最后一部分的内容,因果归纳和机器学习。
总共分四个部分,这是第一部分,讲因果归纳和半监督学习。
关于半监督学习(semi-supervised learning),介绍的人很多,比如参考[2],这里就不专门仔细介绍了,大概就是,在有标签数据+无标签数据混合成的训练数据中使用的机器学习算法吧[2]。
现在我们需要回顾一下MIT因果迷你课笔记 —— 发现因果关系1中RCCP,d-separation和Makov概念。
我们认为一个图是Markov的,如果图中的变量满足:
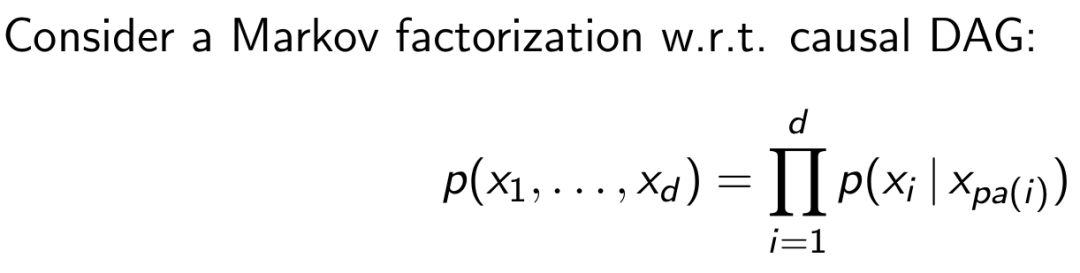
这种时候,如果一个变量的因的值都知道了,那么它应该是独立于其他知道因的变量的:
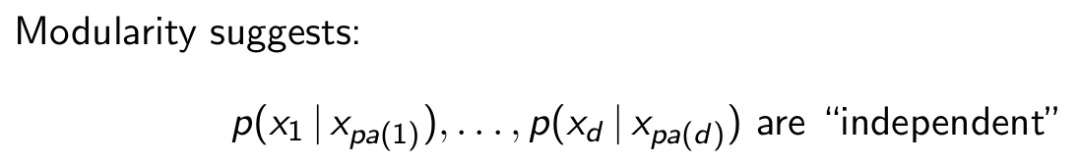
我们可以想象一下变量x1和x2的方程式,应该是有因和噪声组成的,如果因知道了,那么就只剩下噪声了,当然就是互相独立的。
接下来看一个特殊案例:
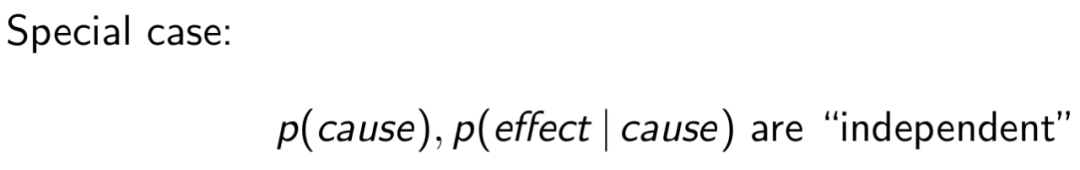
知道了因的果和因是相互独立的。
再来看半监督学习,半监督学习感兴趣的是P(Y|X),即给你X(比如图片),你判断Y(比如图片里有一只狮子)发生的概率是多少。而半监督学习除了通过标注的数据训练模型,还想通过未标注的数据优化模型。如果把图片是因,Y是果,根据上面的理论,P(X)和P(Y|X)相互独立,更多的未标注的图片P(X)并不能为P(Y|X)带来更多的信息量。
因此,根据上面的理论,半监督学习对于X和Y存在严格的因果关系的任务是无效的。接下来看一个实验:
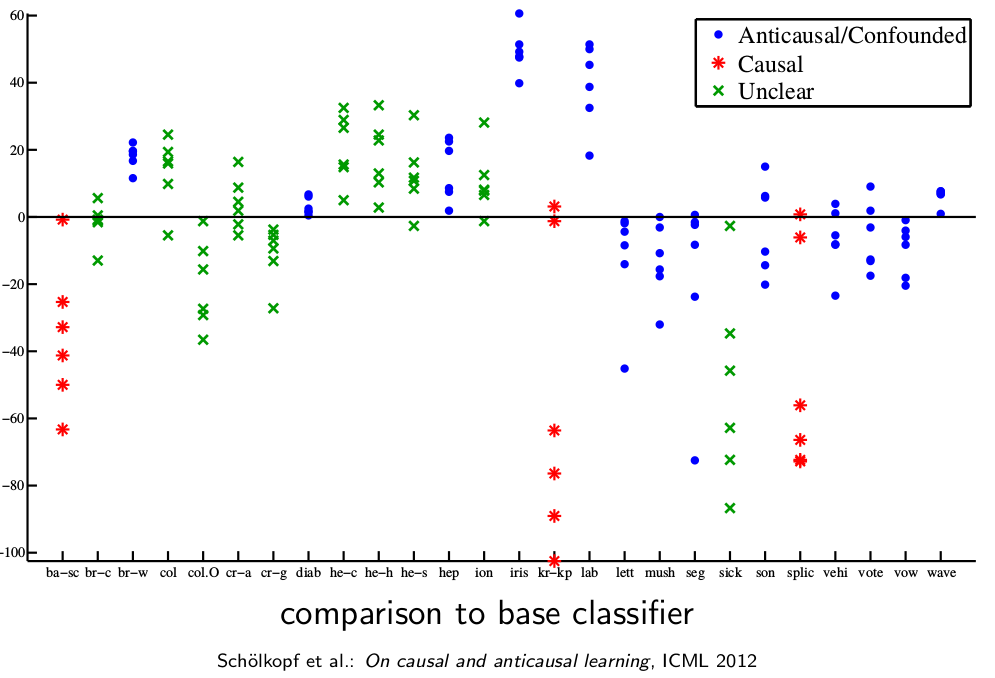
横轴标记了不同的数据集,纵轴则标记了使用未标注的优化模型后,模型的表现,0表示模型准确度没有因为未标注的数据参与优化而变,负值表示准确度反而降低了,正值表示准确度提高了。这里分别介绍一下Anticausal,Confounded,Causal,和Unclear的意思,Anticausal表示数据集中X至少有一个特征是Y的果,Confounded表示X中至少有一个特征和Y有共同的因,这两个要表达的意思是P(Y|X)和P(X)不相互独立,Causal表示,X中只有Y的因,没有Y的果,即P(Y|X)和P(X)相互独立,Unclear很好理解,就是什么因啊果啊的,分不清楚,不知道P(Y|X)和P(X)是相互独立呢还是相关。由上面的实验可知,半监督学习对于标记为Causal的数据集是无效的,但对于很多标记为Anticausal和Confounded的数据集是有效的。
所以在做半监督学习之前,不妨先研究一下数据集的因果关系吧。
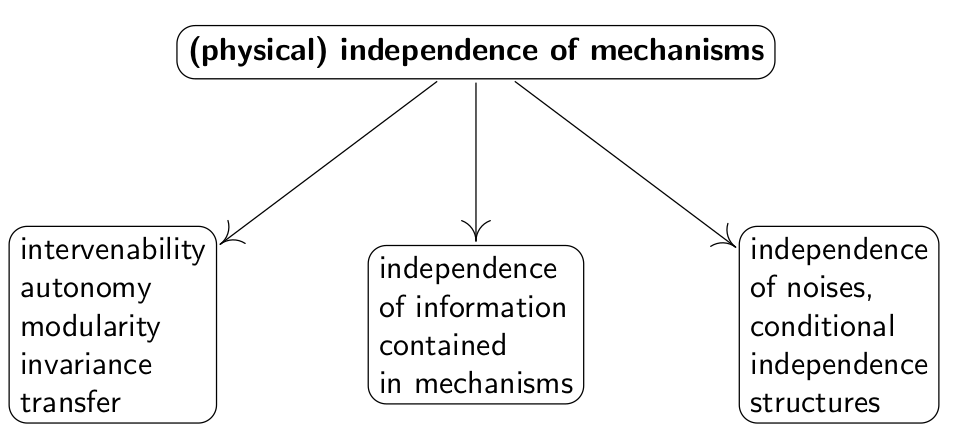
上图是数据独立性判断的一些机制,和判断因果有共通之处,感兴趣的具体可以参考2012年发表在ICML上的论文On causal and anticausal learning,这里就不详细说了。
系列首篇:MIT因果迷你课笔记 —— 相关和因果
上篇:MIT因果迷你课笔记 —— 基于不变性的因果预测(invariant causal prediction)
记:公式上上下下有不匹配的地方,因为截自不同的参考文献,所以写法会有出入,打公式太累了,我放过了自己。
声明:所有图片均来自参考,没有原创图片,公式和定理。
参考:
[1] Jonas Peters, University of Copenhagen, Mini-course on Causality, Laboratory for Information & Decision Systems (LIDS) and Models, Inference & Algorithms of the Broad Institute, MIT, 2017
[2] 糯米稻谷,半监督深度学习小结,知乎,2018
[3] Schölkopf et al., On causal and anticausal learning, ICML, 2012




Comments