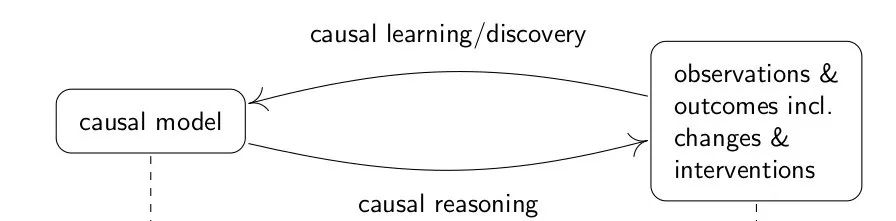
在这门课中,因果模型的形成主要包含因果关系的学习和发现(causal learning/discovery),还有因果关系的推理(causal reasoning)。
课程里先说的是因果关系的推理,即有了因果模型,去推导结果或者干预后的状况。接下来说因果关系的发现。
因果关系的发现内容复杂,逻辑绕,可能会分两到三篇来说,这里是第一篇。
因果关系的发现,即从数据中发现因果关系,那么怎么从数据中归纳因果关系?
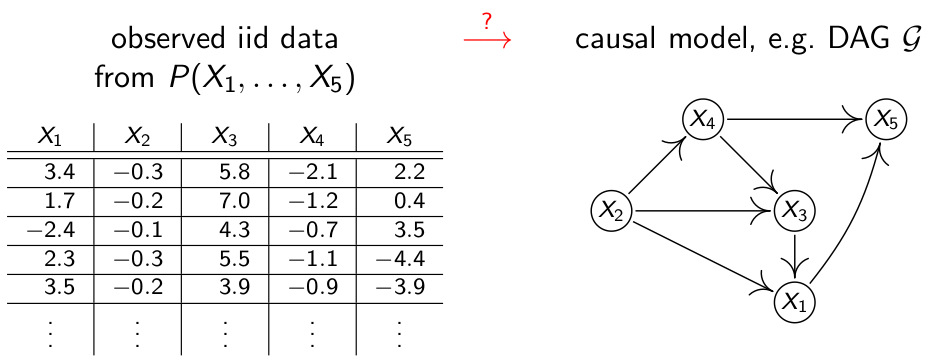
首先来了解一些基本概念。
RCCP **(Reichenbach’s Common Cause Principle), 是Hans Reichenbach死后出版的一本未完成的书《The Direction of Time**》中提出的概念。假设我们现在有两个事件,A和B,如果p(A∩B)>p(A)p(B)说明事件A和B不相互独立,即两个事件相关,那么相关和因果是什么关系呢?Reichenbach’s Common Cause Principle (RCCP) 认为如果p(A∩B)>p(A)p(B),且A不是B的因,B也不是A的因,那么A,B应该有共同的因。
概念定义如下:

A、B是两个事件,如果:
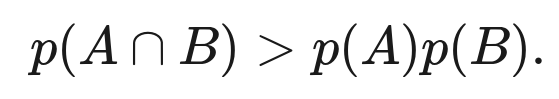
遵循RCCP原理,则A是B的因,或者B是A的因,或者A,B有共同的因,在第三种情况下,如果共同因事件是C,那么A和B则是有条件的独立:
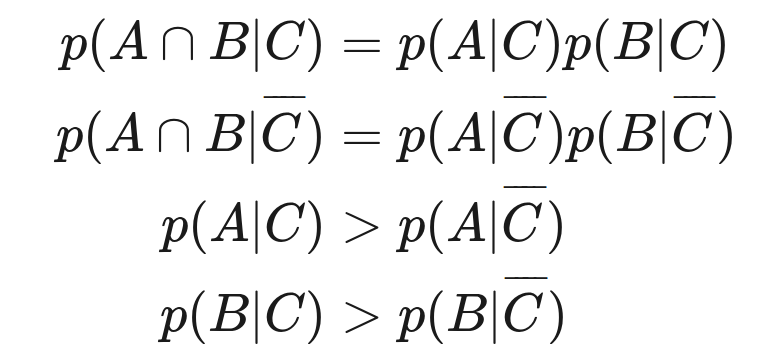
RCCP的概念还有很多可追究的地方,推荐斯坦福的一篇文章,这篇文章甚至还描述了RCCP在量子力学中的地位,有机会可以专门开个坑说一下这些概念,https://plato.stanford.edu/entries/physics-Rpcc/。
接下来说一下图的定义:
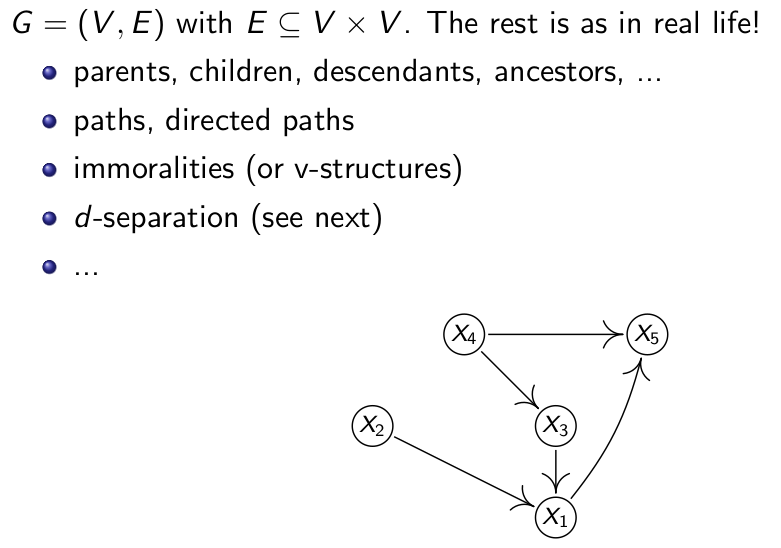
图由点和边构成,图可以是有向图和无向图,这个课程里的图基本都是有向图,在图形上的表现就是边是有箭头的,有指向的。v-structure是说,比如X2和X3均指向X1,但是X2和X3之间却没有直接的关联,这种结构就被称之为immorality。
d-separation, 一个和图还有RCCP相关的非常重要的概念,因为相对复杂,所以专门写了一篇**D-separation,d-connection**,一定要先看这篇。
Causal Markov Condition 有很多种定义方式,基于d-separation的定义方式如下:
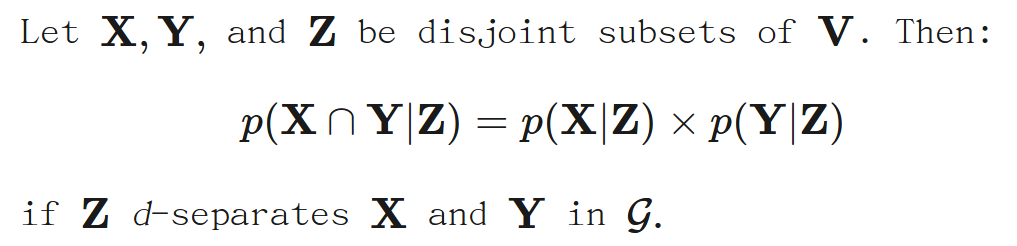
换种写法如下,P是变量的分布情况(distribution),w.r.t. (with respect to) G表示这组变量之间的因果关系是按G图表示的那样:

我们认为分布P是Markov的,如果Xi和Xj在图G中被S d-separated能推导出Xi⊥Xj |S。在这里我们用⊥代替图中的独立符号,因为图中的独立符号在这里打不出来。
我们回想一下RCCP的概念,则不难得出,马可夫状态是RCCP的一般化的形式。另外,马可夫状态还有其他两种定义方式:
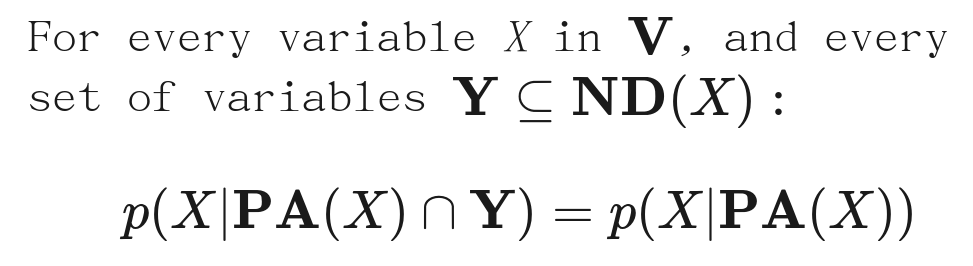
其中Y是一组变量的集合,PA(X)指X的所有的父变量的集合,ND(X)指除了X变量和其后裔变量之外的所有变量的集合。下面这种是基于分解的定义方式:
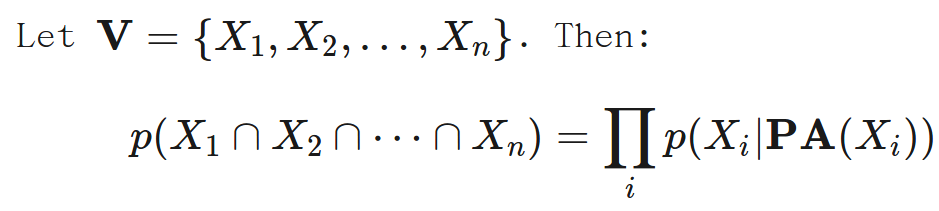
这几种定义方式是等价的。
假设现在你获得了一批数据,你可以很容易得到各个变量的分布,即P,换言而之,你可以很轻松地知道Xi⊥Xj |S是否成立,现在你想通过分布推导出因果关系,那么可以用前面的Causal Markov Condition吗?明显不行,因为箭头是单向的,可以由d-separation推导出分布,但不能根据上面的定理推导出d-separation。
为了可以反过来推导,我们定义了一个假设:
faithfulness assumption,这个概念和马可夫是一个对应的概念,注意下面推理的箭头,和马可夫概念中推理的箭头是反方向。这个假设使我们可以通过分布来推导因果关系。如果可以反过来推,我们认为P faithful。

现在我们来做几道题,辅助理解一下上面的两个概念,我们假设P是markov且faithful w.r.t. G,现在P有如下几种状况,请分别推导出对应的因果图G:
(i)X⊥Z **(vars: **X, Y,Z)
(ii)X⊥Y|Z **(vars: **X, Y,Z)
(iii)X⊥Y,X⊥W|Z **,Y⊥W|Z ,X⊥W|Z, **Y,Y⊥W|Z, **X **(vars:X,Y,W, Z)
以上三种情况对应的G可以是(一种d-separation的状况可以匹配多个因果图):
(i)X->Y<-**Z **
(ii)X->Z->Y;X<-Z<-Y;X<-Z->Y。
(iii)(X->Z)&(Y->Z->W)
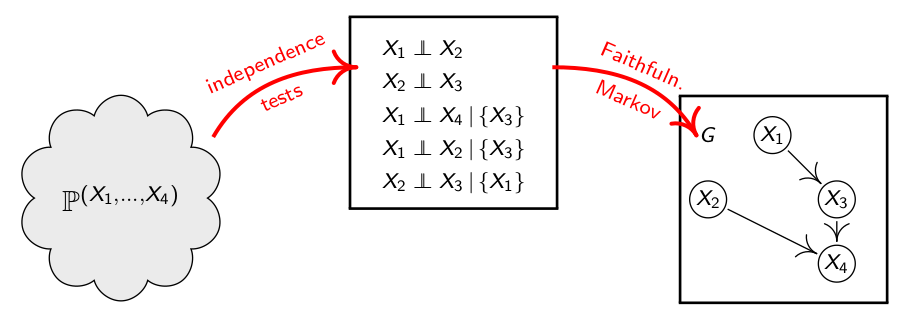
要得到因果图,从P中,首先找出所有的独立关系,和相对独立的关系,再根据Markov和Faithfulness的假设得到因果关系。
通过以上的例子,我们发现,一种d-separations的情况可以得到不同的因果图:
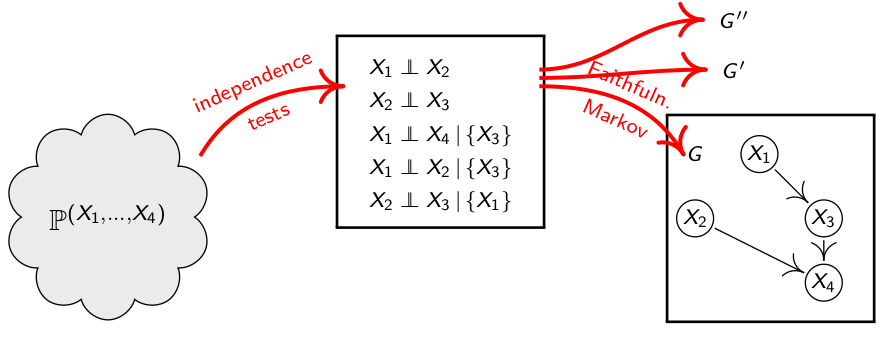
我们称这些由同样的d-separations的状况得到的因果图为Markov Equivalence的,反过来说就是,
Def:如果两个因果图能得到同样的d-separations,则称这两个图为Markov Equivalence的,是基于马可夫等价的。
再来看由此得到的一个命题:
Prop:(Verma & Pearl)因果关系图G,H是Markov Equivalence <=> G和H有相同的骨架,和v-structrues。
可以对照上面三个案例来验证一下这个命题。
有P对于某个G不是faithful的案例吗?当然是有的,如果G是这样的:
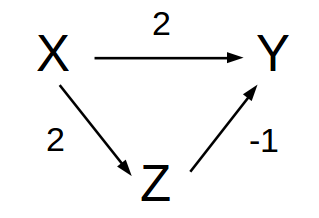
那么,Y =2X - Z + Ny = 2X - 2X - Nz+ Ny = Ny - Nz,所以X⊥Y,但是却并不能得到X和Y被一个空集d-separated的结果。简而言之,faithfulness的假设将这个世界的状况简化了,真实世界的数据是十分复杂的。
接下来,我们来回顾我们之前见过的一个案例:
案例:夜间照明和小孩患近视的因果关系

由统计数据可以知道,为孩子提供夜间照明和小孩患近视这两件事情是相关的。根据RCCP原理,要么这两件事存在因果关系,要么它们有共同的因。而通过调查得到一个d-separation,night light ⊥ child myopia | parent myopia,即night light (NL)和child myopia (CM)可以被parent myopia (PM) d-separated。所以,根据faithfulness的假设,这三件事之间的关系可能是:
(i) NL->PM->CM
(ii) CM->PM->NL
(iii) CM<-PM->NL
由于(i)和(ii)可以用常识来否定,给孩子的夜间照明不能够成为大人近视的因,孩子的近视不能够成为大人近视的因,因此最后得到的因果关系是:
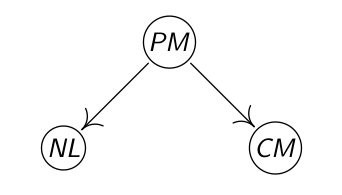
以上,我们知道,通过数据分布P得到的d-separations的状况,可以让我们得到一组Markov Equivalence的因果图,那么接下来一个显而易见的问题是,如何区分Markov Equivalence的因果图。如上例,我们怎么知道X,Y,Z之间的因果关系是X->Z->Y,或是X->Z->Y,或是X<-Z->Y,显然,在同一个现实场景中,这三种因果关系不可能同时成立。那么究竟是哪一个呢?如何才能知道是哪一个呢?除了像上例一样依靠常识来排除,还有其他可行的方法吗?
声明:所有图片均来自参考,没有原创图片,公式和定理。
参考:
[1] Jonas Peters, University of Copenhagen, Mini course on Causality, Laboratory for Information & Decision Systems (LIDS) and Models, Inference & Algorithms of the Broad Institute, MIT, 2017
[2] https://www.andrew.cmu.edu/user/scheines/tutor/d-sep.html
[3] https://plato.stanford.edu/entries/physics-Rpcc/
[4] Judea Pearl and Dana Mackenzie, The Book of Why, 2018




Comments