交叉熵度量的是两个概率分布的差异。
要理解交叉熵,有很多小概念需要理解。
信息量,一个事件发生的概率越大,事件发生携带的信息量越小,发生的概率越小,事件发生携带的信息量越大。比如太阳从东边升起,这个事件如果发生了,我们可以从这个事件中获得的信息几乎是没有的。但是,如果哪天太阳从西边升起了,那么我们从这个事件中获得的信息量是极大的,一定发生了什么,或者即将发生什么,才造成了这个事件发生。
假设X是一个离散型随机变量,概率分布函数为:
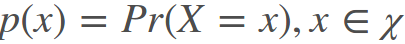
则定义X = x0事件发生携带的信息量为:
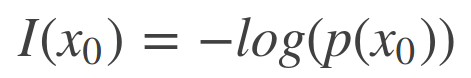
若p(x0)为0,也就是事件x0是不可能发生的事件,但是它却发生了,那么这个事件的信息量是无穷大的,I(x0)的值无穷大,如果p(x0)为1,也就是事件x0是一定会发生的事件,那么这个事件的发生是不带信息量的,I(x0)的值是0。
另外,信息量可以这样理解 [2]:
Information quantifies the number of bits required to encode and transmit an event.
信息量可以被理解为,传输或表达这个信息需要的编码的位数。
信息熵,则是信息量的期望值:
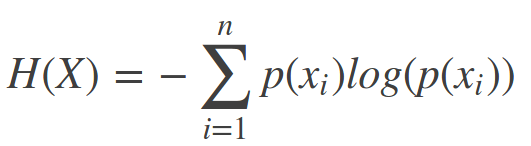
参考[3]里给了一个例子:
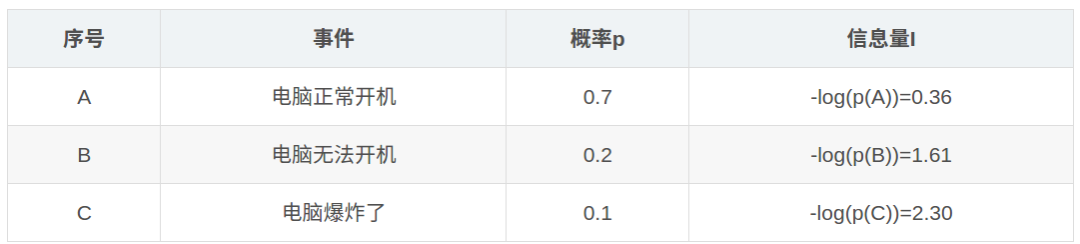
每次开电脑,都可能会产生三种状况,电脑正常开机的概率是0.7,电脑无法开机的概率是0.2,电脑爆炸的概率是0.1。那么每次开机,得到的信息量的的期望值是:
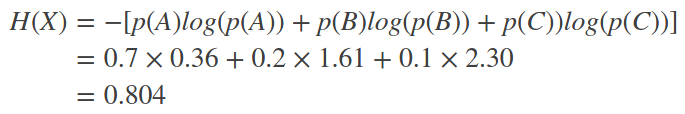
如果是二项分布,那么信息熵的计算可以简化为:
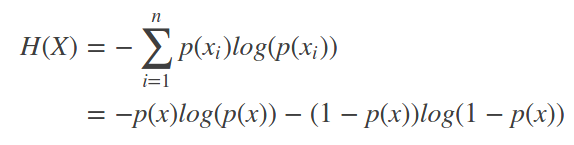
事件的概率不均,信息熵较小,若各个事件发生的概率一样,信息熵较大。
信息熵在[2]中的描述为:
Entropy is the number of bits required to transmit a randomly selected event from a probability distribution.
熵是表达或者传输一个遵循特定概率分布的随机事件需要的位数,个人觉得the number of应该改成the average number of,位数前面应该有个平均,和期望的概念对应上。但也可能是我哪里理解错了。
相对熵(relative entropy),又称之为KL散度(Kullback-Leibler (KL) divergence),公式:
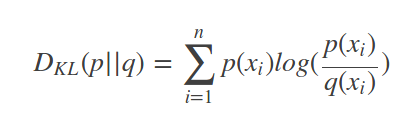
相对熵的目标是:计算用P描述目标问题,比Q描述目标问题能获得的信息增量。
如果分布P和分布Q是一样的,那么相对熵是0,如果不一样,相对熵大于0,越大,表示两种分布之间的差距越大。
在机器学习的项目中,通常P表示真实的分布,即需要训练模型达到的分布,Q是现在用的模型预测的分布。
相对熵在参考[2]中的描述是:
In other words, the KL divergence is the average number of extra bits needed to encode the data, due to the fact that we used distribution q to encode the data instead of the true distribution p.
— Page 58, Machine Learning: A Probabilistic Perspective, 2012.
相对熵是,当我们用分布q来替代事件真实遵循的分布p时,传输和表达事件时,比使用分布p多需要的平均位数。也就是q是我们用的分布,p是事件真实遵循的分布,用q的话,比用p需要更多的位数来表达和传输这个事件,平均多多少呢,相对熵就是这个多出来的多少。
交叉熵(Cross entropy),将相对熵公式变形:
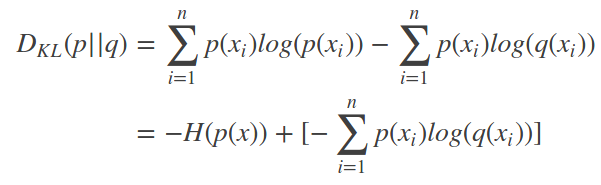
前半部分是信息熵的负值,后半部分则是交叉熵,交叉熵的公式是:
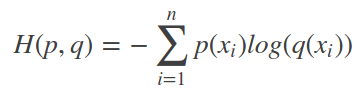
因为P的信息熵是一定的,那么其实是可以省略这部分计算的,交叉熵和相对熵的意义是一样的。只是最后计算出的值,区间不一样。
交叉熵在参考[2]中的描述是:
…, the cross entropy is the average number of bits needed to encode data coming from a source with distribution p when we use model q, … — Page 57, Machine Learning: A Probabilistic Perspective, 2012
交叉熵是当你用模型q来预测分布p时,表达和传输事件需要的平均位数。
以下定义来自参考[2],俺就不翻了:
- Cross-Entropy: Average number of total bits to represent an event from Q instead of P.
- Relative Entropy (KL Divergence): Average number of extra bits to represent an event from Q instead of P.
Cross-Entropy Loss 和 Softmax Loss
毫无疑问,交叉熵可以用作损失函数,且比起MSE,MAE,要优秀不少,
… using the cross-entropy error function instead of the sum-of-squares for a classification problem leads to faster training as well as improved generalization. — Page 235, Pattern Recognition and Machine Learning, 2006.
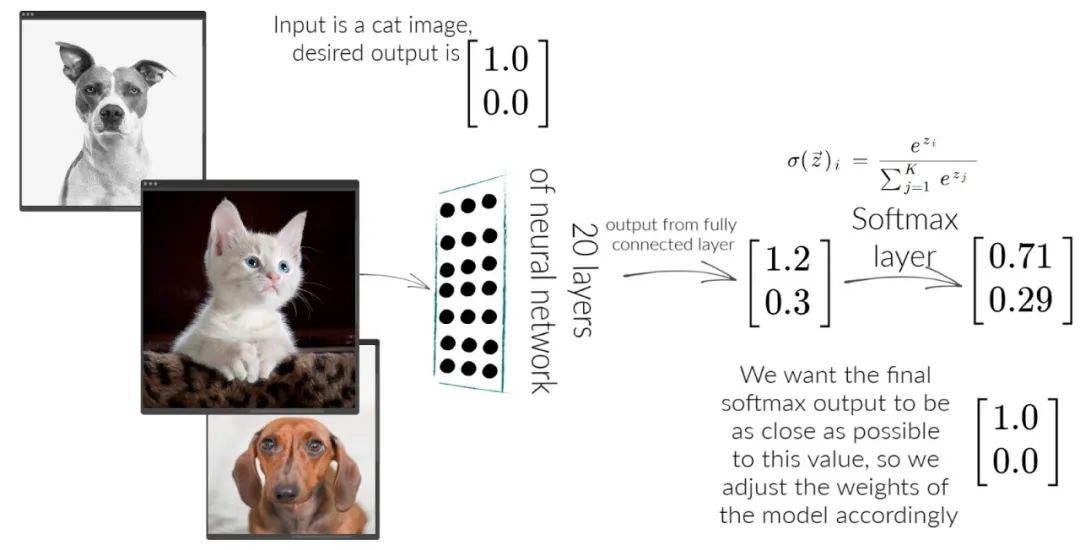
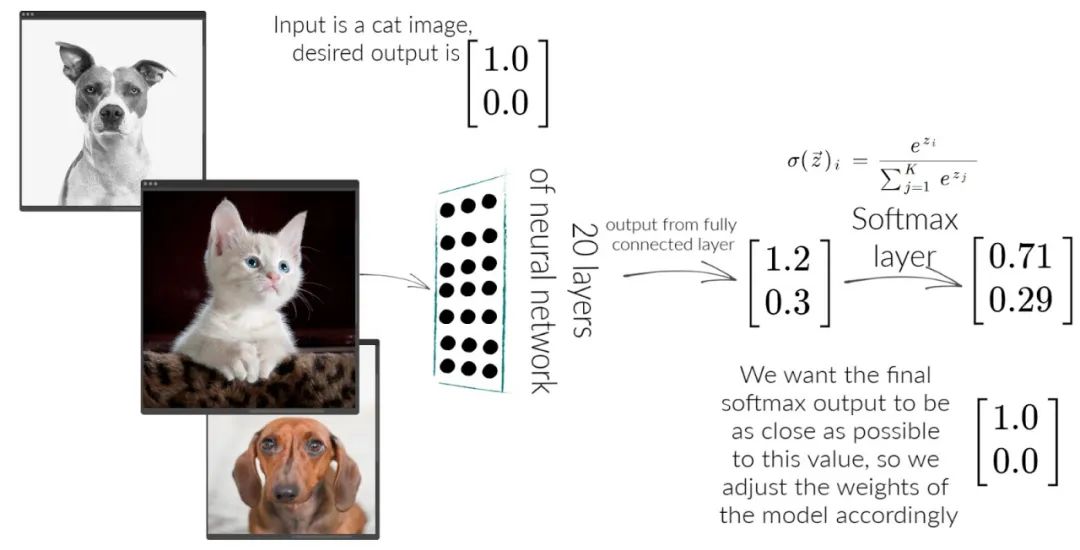
结合上面猫狗分类的案例,假如有一张猫图输入,P是[1, 0], Q是[0.71, 0.29],交叉熵的计算为:
H(P, Q) = – (P(cat) * log(Q(cat)) + P(dog) * log(Q(dog)))
值得注意的是,在很多多分类问题中,不论有多少类,P不论有多少个元素,都只有一个为1,其他都为0,所以交叉熵的计算可以化简,也就是说如果P(cat)为1,那么交叉熵的结果和Q(dog),Q(car),Q(any other)是无关的:
H(P, Q) = – log(Q(cat))
因此,如果Q(cat)是用Softmax Function计算出来的,那么H(P, Q)计算得到的就是该样本在该模型下的Softmax Loss。
Softmax Loss的完整公式如下:
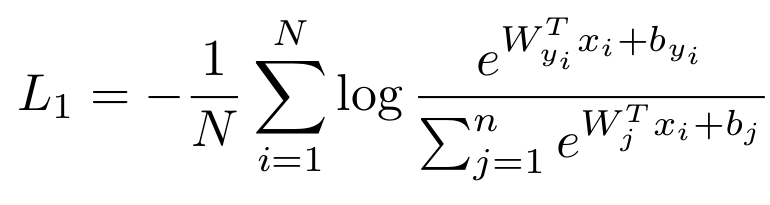
N是样本数量,n是class的数量,特征向量的长度为d,Wj是W的第j列,和b一起是获得特征向量的全连接层,W是d*n,bj的长度是n。log后面则是用Softmax Function计算出的‘Q(cat)’。
因此,其实本来没有什么Softmax Loss的概念,这个公式是在多分类任务中使用Softmax Function+Cross Entropy loss产生的。
Cross Entropy Loss 和 Log Loss [4]
她俩在解决二分类问题的时候,其实是一回事,不服气的看公式:
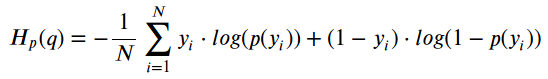
这个公式既叫Binary Cross-Entropy,也叫Log Loss,y是label,p(y)是预测结果,符号和之前的公式没有一一对应,看的时候注意一下。
Log Loss的推导基于最大似然估计(Maximum Likelihood)和伯努利分布(Bernoulli distribution),有机会写一篇。
那么Cross Entropy的值为多少时,表示预测的结果还挺准确的呢?这里参考[2]给了个一些参考,具体问题还要具体分析。
- Cross-Entropy = 0.00: Perfect probabilities.
- Cross-Entropy < 0.02: Great probabilities.
- Cross-Entropy < 0.05: On the right track.
- Cross-Entropy < 0.20: Fine.
- Cross-Entropy > 0.30: Not great.
- Cross-Entropy > 1.00: Terrible.
- Cross-Entropy > 2.00 Something is broken.
参考:
[1] Thomas Wood,Softmax Function Definition, DeepAI
[2] Jason Brownlee,A Gentle Introduction to Cross-Entropy for Machine Learning,2019
[3] 史丹利复合田,一文搞懂交叉熵在机器学习中的使用,透彻理解交叉熵背后的直觉,CSDN,2018
[4] Daniel Godoy, Understanding binary cross-entropy / log loss: a visual explanation, Towards Data Science, 2018


的设计/28.png)
Comments